According to Adding It Up (H/T Dan Meyer):
Conceptual understanding refers to an integrated and functional grasp of mathematical ideas. Students with conceptual understanding know more than isolated facts and methods. They understand why a mathematical idea is important and the kinds of contexts in which is it useful. They have organized their knowledge into a coherent whole, which enables them to learn new ideas by connecting those ideas to what they already know. Conceptual understanding also supports retention. Because facts and methods learned with understanding are connected, they are easier to remember and use, and they can be reconstructed when forgotten. (pp. 118-119.)
Essentially, conceptual understanding is knowing more than isolated facts, it is also knowing connections between those facts and having those facts well organized.
This image represents someone who understands some isolated facts.

And this image represents what conceptual understanding looks like:
I propose that those line segments between the points, representing the connections between isolated knowledge, are themselves a type of knowledge, consequently our second image is really more like the first image.
What is clearly missing in this analogy is that conceptual understanding is knowledge that is well-organized, but I claim that organization of knowledge is itself another type of knowledge. Also missing is knowing why the knowledge is important and the contexts in which an idea are useful, but again these also seem just like other types of knowledge.
Let’s take a look at a problem I had to solve recently and see if we can use it to unpack what conceptual understanding is.
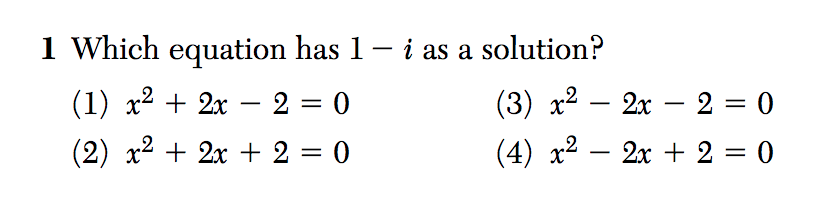
According to the solution key, the writers of this question are assessing students’ ability to solve quadratic equations. However, that likely requires applying the quadratic equation to all four equations given, which would be time-consuming and potentially error-prone.
When I solved this problem, I saw four quadratic functions, each transformed from y = x2, and based on those transformations, I was able to eliminate (1) and (3) as options since they have real solutions. I also know that if 1 – i is a solution, then so is 1 + i, and that the sum of the roots of a quadratic function are related to the coefficient of x in the equation. I could not remember if the sum of the roots is equal to the coefficient of x or to -1 times the coefficient of x, so I multiplied out (x – a)(x – b) to double-check and determined that if a and b are the roots of a quadratic equation, then -(a + b) is the coefficient of x in that equation (assuming a lead coefficient in the equation of 1). 1 – i + 1 + i = 2 so (4) must be the answer.
My actual solution strategy doesn’t matter all that much, what matters is that in order to produce it, I needed to know some smaller things and that those smaller things could be seen as connected together to create a larger idea. Instead of seeing this as the difference between an expert and a novice, I prefer to think of knowing things as being a gradient between knowing a little bit and knowing more than a little bit.
Conceptual understanding is both knowing ideas in an interconnected and organized way and knowing more ideas along the novice-expert spectrum.
The reason why conceptual understanding is an important goal is because otherwise we might be tempted to rely on teaching kids tricks instead of mathematics.
What mathematics does a child learn from learning this procedure for adding fractions?
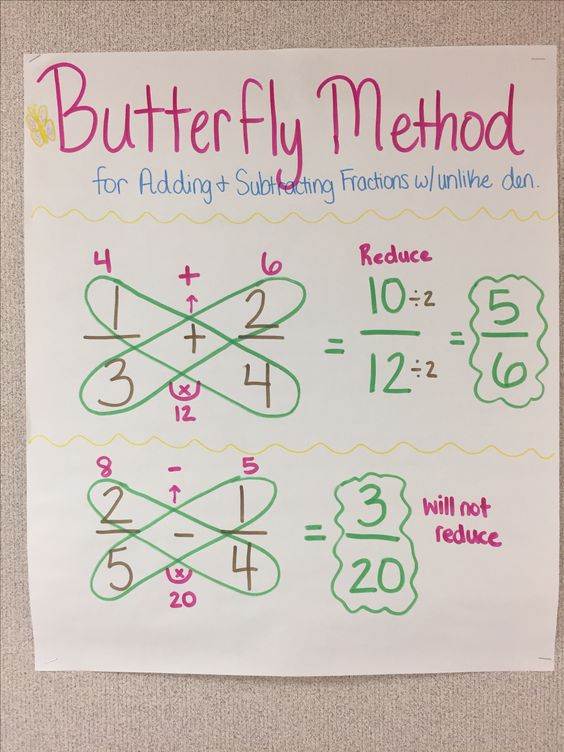
Source: Pinterest
Very little! It is extremely difficult for a child to connect this procedure to other mathematics that they know, consequently using a trick like the butterfly method is likely to lead to students knowing an isolated idea and not much else. Note that I am not opposed to memory aids, I just think they should be based on solid mathematical reasoning and they definitely should not be taught instead of the mathematics.