An experiment
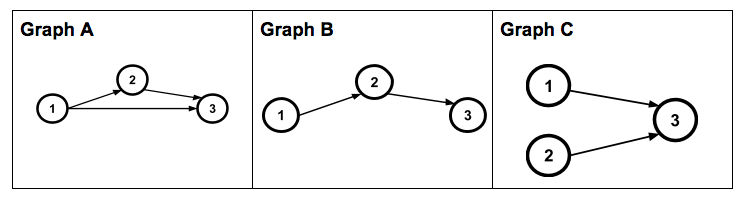
Let’s try a little experiment. Take a look at the following network graphs and think about what is different for each graph and what is the same for each graph.
Now look at this matrices associated with these network graphs.
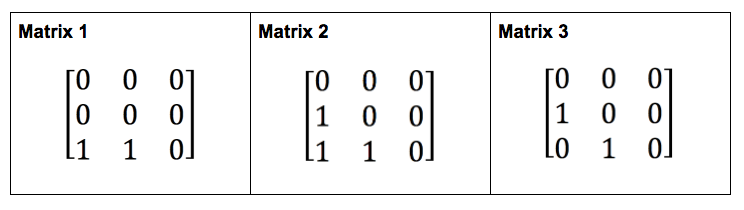
Which network graph do you think goes with which matrix and why? (This might take you a few minutes. Be patient.)
This particular task is intended to be used with an instructional routine called Connecting Representations designed by Amy Lucenta and Grace Kelemanik. They describe this instructional routine and three other instructional routines in significant detail in the book they just published, Routines for Reasoning.
One goal of Connecting Representations is to support students in making connections between different mathematical representations which describe the same mathematics but on the surface look very different. Another goal of the routine is to support students in being able to see and describe the mathematical features (or structure) that are important to pay attention to in the individual representations in order to make connections between representations.
In the network graphs, as you no doubt noticed, the number of nodes, the labels for the nodes, the ways arrows are connected between nodes, and the direction of those arrows are all important features. You may have concluded as well that the actual positions of the nodes do not matter. Additionally, by looking at the network graphs and this paragraph, you may also know exactly which parts of the graphs I mean by the word ‘node’ (if not, I mean the circles with the numbers inside).
In the matrices, if you make connections between the graphs and the matrices, you almost certainly had to pay attention to the rows and columns of the matrices and the values of the entries in the matrices, most of which were zeros and some of which were ones.
At a meta-level, you focused on individual parts of each representation, you may have zoomed out to look across different representations, and you made connections between different representations.
Variation theory
I’ve recently been attempting to incorporate a critical idea from variation theory into the design of curricular resources; students learn from noticing differences across a background of sameness, rather than from seeing similar objects and discerning the important features by what is the same across each of the objects. Another way of saying this is that differences stand out much more than similarities do.
On Variation theory, Mun Ling Lo writes:

For the network graphs above, I deliberately varied the connections between nodes and the position of the nodes within the diagram. In the matrices, I represented the connections between nodes and did not represent the position (since I cannot represent the position in a matrix) which resulted in a deliberate variation across the rows and columns.
Tasks that are not really learning tasks
Not all tasks are tasks that students will make new connections from. Some tasks require students to demonstrate understanding of a concept they already know. While it is helpful for students to rethink about ideas periodically as there is significant evidence that this helps students remember ideas over time, we also need to use tasks that build new understanding.
Here’s an example of a task on the same content that assumes students know some mathematical ideas already.
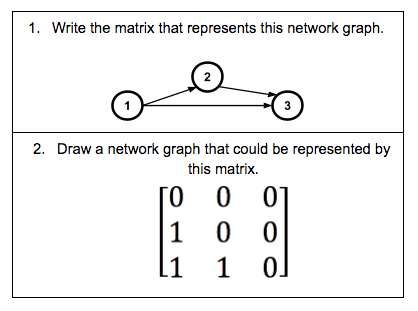
Note that it is impossible for students to do this task without already knowing how to answer both questions. This is not a task that students are likely to learn something new from on its own.
Side note: This is by the most common kind of task I see when I have observed teachers over the past five years.
Instructional efficiency
One strategy for taking a task that serves both purposes of helping students remember things they have learned before and helping students build new connections is to have students practice solving problems but deliberately sequence the problems so that students see new connections between the problems they solve.
For example, try and solve the following mental arithmetic problems in your head, without a calculator, and without writing anything down. While solving these problems, deliberately try to use what you’ve done in an earlier problem to make the next problem easier to solve.
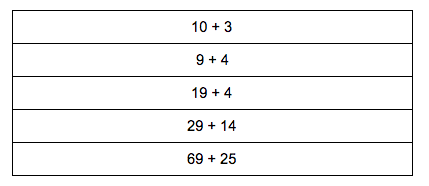
What did you notice yourself doing as you worked through the problems? What big idea might students get out of solving this series of problems?
Ideally you saw that 10 + 3 is the same as 9 + 4 and that may have helped you see 9 + 4 as 9 + 1 + 3 = 10 + 3 so that you could reuse your solution to the previous problem. For 19 + 4, you may have also regrouped to 19 + 1 + 3 = 20 + 3. 29 + 14 may have become 30 + 13 = 43 and 69 + 25 may have become 70 + 24. If not, then if I wanted you to see this, as a teacher I may have had a student who did regroup like this share their strategy with the class.
My point is that I have increased the odds that you saw this regrouping strategy by deliberately choosing the problems for you to try.
Conclusion:
If you are designing curriculum or tasks for your students here are my two recommendations:
- Pay attention to what you are varying across different problems or representations you give students. What you vary across a group of related problems or representations is what students are more likely to notice.
- If possible, do this even when giving students problems to practice so that there is a chance students learn something new from that practice.









