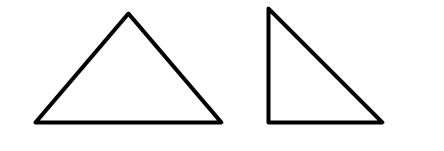Year: 2016 (page 1 of 2)

“Mathematics is not done with a computer. Mathematics is not done with pencil and paper. Mathematics is done with the brain.”

~ An anonymous participant of the Computer Based Mathematics Summit, London, 2011

The heart of mathematics education is ensuring that students develop both knowledge of mathematics (here is a definition of mathematics) and productive dispositions towards mathematics. The minimum test for us to apply when considering the use of technology in mathematics education is this: “How does this use of technology help develop students’ knowledge of mathematics and/or their productive dispositions towards mathematics?”

An early form of technology for mathematics, source : Wikipedia

There are five traps to avoid when using technology. The first trap is that students end up not learning mathematics but instead only learning how to use a particular technological tool. The second trap is that someone who knows the mathematics already can see the mathematical principles illustrated by a particular technological tool but that a novice does not see or use the tool the same as the expert and therefore does not experience the mathematics the same. The third trap is using technology solely to focus on recall and repetition since students often lose opportunities to see patterns across problems (it doesn’t do much for most students’ productive dispositions towards mathematics either). The fourth trap of technology is that it can isolate learners, both from each other and sometimes even from their teacher. The final trap is that technology can sometimes make it harder to see (or hear) how students understand mathematical ideas.

Here are some questions we should ask ourselves when deciding to use any particular piece of technology with our students:

• Does using this technology help my students learn mathematics that they can use without the use of this technology?
• How will someone who does not yet know the mathematics embedded within this technological tool see the mathematics?
• Does this technology focus solely on the acquisition of a limited set of mathematical knowledge or is it possible for students to use deliberate practice to identify patterns across different problems and acquire new mathematical ideas?
• Does this technology make it harder for my students to interact with each other and with me?
• How will I learn how my students understand the mathematical ideas that are the focus of this lesson?

In a follow-up post, when I have more time, I’m hoping to share examples of technologies that fall into these traps and how I might change the technologies to avoid the trap or how I might change might change my teaching to circumvent the trap.

In an age where fake news is beginning to dominate the media consumed by millions of people around the world and Google’s results are being gamed by racist organizations, claiming that students don’t need to know anything because “they can just Google it” is irresponsible at best and negligent at worst.

Students (and adults) are struggling to determine what’s real and what’s not. We need to do more as educators than just surface that fake news exists (like the Northwest Tree Octopus). We must ensure that our children leave school knowing enough history, geography, math, science, language, etc… so that they cannot be easily be fooled by fake news.

The best inoculation against misinformation is a rich base of knowledge and experience that contradicts that misinformation.

Teachers do a lot of marking of student work. But is it necessary?

(source)

In this comprehensive review of the literature on feedback, corrective feedback (example shown below) without mechanisms for correcting that feedback were found, unsurprisingly, to have little impact on student learning in most cases.

An example of minimal feedback

Unfortunately, there is also good evidence (see the same literature review) that taking even more time to add comments to student work does not lead, by itself, to improved student learning. So what can teachers do differently?

"When you grade, you help one child at a time. When you plan, you help all kids. Spend your time accordingly." ~ @hpicciotto #NCTMregionals

— David Wees (@davidwees) October 28, 2016

Here’s a simple strategy. Take a pile of student work and review it, looking for evidence of student performance, and find examples of feedback that you can meaningfully target to groups of students, and then design activities for the whole class to do that result in different groups of students getting feedback on their ideas. In other words, integrate the time you would spend marking with the time you spend planning but in response to what students did in your class.

One question that comes up when I suggest this strategy to teachers is “But what will I put in my grade-book?” Here I suggest that a grade-book can contain evidence of completion of tasks on a regular basis and that for a smaller number of assignments, more detailed information could be provided. Stopping grading everything doesn’t mean you can’t grade anything; just be more selective. A more radical suggestion is to work at the school-wide level and eliminate everything that isn’t absolutely necessary to improve student learning.

It is well known that children often struggle to solve word problems in mathematics. One strategy that is used to support students with having access to word problems is called CUBES. Another is to have students identify all of the keywords in the problem. (Update: Margie Pearse wrote a longer response to these same two strategies here).

In these strategies, students are encouraged to chunk the information given in the word problem in a variety of different ways. For the CUBES strategy, the word quantities is often defined as numbers including units and direction (if given).

Let’s try out the CUBES strategy with the following word problem from the Mathematics Assessment Project. Why don’t you try it yourself first?

Here is my attempt, as if I were a student, on this task for just the first three of the steps in CUBES.

You’ll notice that I have circled a lot of unimportant quantities. I’ve also boxed some math words or expressions that are probably not helpful. These are reasonable things to expect many students to do. How does a child know that “three-course meal” is really a description of a kind of food and not a quantity in this context? We could easily imagine contexts in which the number of courses in a meal is important.

My point is that CUBES is an insufficient strategy to help students have entry to this problem. It might be helpful (sometimes) but it almost certainly not sufficient. There is a lot of thinking yet to be done before identifying the critical information from the problem and being able to solve the problem.

Here are some additional recommendations that you can combine as needed:

An experiment

Let’s try a little experiment. Take a look at the following network graphs and think about what is different for each graph and what is the same for each graph.

Now look at this matrices associated with these network graphs.

Which network graph do you think goes with which matrix and why? (This might take you a few minutes. Be patient.)

This particular task is intended to be used with an instructional routine called Connecting Representations designed by Amy Lucenta and Grace Kelemanik. They describe this instructional routine and three other instructional routines in significant detail in the book they just published, Routines for Reasoning.

One goal of Connecting Representations is to support students in making connections between different mathematical representations which describe the same mathematics but on the surface look very different. Another goal of the routine is to support students in being able to see and describe the mathematical features (or structure) that are important to pay attention to in the individual representations in order to make connections between representations.

In the network graphs, as you no doubt noticed, the number of nodes, the labels for the nodes, the ways arrows are connected between nodes, and the direction of those arrows are all important features. You may have concluded as well that the actual positions of the nodes do not matter. Additionally, by looking at the network graphs and this paragraph, you may also know exactly which parts of the graphs I mean by the word ‘node’ (if not, I mean the circles with the numbers inside).

In the matrices, if you make connections between the graphs and the matrices, you almost certainly had to pay attention to the rows and columns of the matrices and the values of the entries in the matrices, most of which were zeros and some of which were ones.

At a meta-level, you focused on individual parts of each representation, you may have zoomed out to look across different representations, and you made connections between different representations.

Variation theory

I’ve recently been attempting to incorporate a critical idea from variation theory into the design of curricular resources; students learn from noticing differences across a background of sameness, rather than from seeing similar objects and discerning the important features by what is the same across each of the objects. Another way of saying this is that differences stand out much more than similarities do.

On Variation theory, Mun Ling Lo writes:

For the network graphs above, I deliberately varied the connections between nodes and the position of the nodes within the diagram. In the matrices, I represented the connections between nodes and did not represent the position (since I cannot represent the position in a matrix) which resulted in a deliberate variation across the rows and columns.

Tasks that are not really learning tasks

Not all tasks are tasks that students will make new connections from. Some tasks require students to demonstrate understanding of a concept they already know. While it is helpful for students to rethink about ideas periodically as there is significant evidence that this helps students remember ideas over time, we also need to use tasks that build new understanding.

Here’s an example of a task on the same content that assumes students know some mathematical ideas already.

Note that it is impossible for students to do this task without already knowing how to answer both questions. This is not a task that students are likely to learn something new from on its own.

Side note: This is by the most common kind of task I see when I have observed teachers over the past five years.

Instructional efficiency

One strategy for taking a task that serves both purposes of helping students remember things they have learned before and helping students build new connections is to have students practice solving problems but deliberately sequence the problems so that students see new connections between the problems they solve.

For example, try and solve the following mental arithmetic problems in your head, without a calculator, and without writing anything down. While solving these problems, deliberately try to use what you’ve done in an earlier problem to make the next problem easier to solve.

What did you notice yourself doing as you worked through the problems? What big idea might students get out of solving this series of problems?

Ideally you saw that 10 + 3 is the same as 9 + 4 and that may have helped you see 9 + 4 as 9 + 1 + 3 = 10 + 3 so that you could reuse your solution to the previous problem. For 19 + 4, you may have also regrouped to 19 + 1 + 3 = 20 + 3. 29 + 14 may have become 30 + 13 = 43 and 69 + 25 may have become 70 + 24. If not, then if I wanted you to see this, as a teacher I may have had a student who did regroup like this share their strategy with the class.

My point is that I have increased the odds that you saw this regrouping strategy by deliberately choosing the problems for you to try.

Conclusion:

If you are designing curriculum or tasks for your students here are my two recommendations:

1. Pay attention to what you are varying across different problems or representations you give students. What you vary across a group of related problems or representations is what students are more likely to notice.
2. If possible, do this even when giving students problems to practice so that there is a chance students learn something new from that practice.

When my son was initially learning about fraction notation, he told me the following, right at the end of a class.

My son: Daddy, 1/3 is the same as 3/4.

Me: Why is that?

My son: The 3 in the denominator tells you how many quarters there are in the fraction.

Wait a minute! 1/3 is not equal to 3/4.

Strictly speaking, this is not evidence that my son learned anything about fractions in that class. This is just a single performance. Many people would say that in this performance, my son failed to demonstrate an understanding of fraction notation.

The goal of teaching though is not to generate specific student performances. The goal of teaching is to produce long-term changes in what students know and can do. While we study performances in classes and use these to make short-term decisions about what to with our students, we should also systematically compare these short-term performances with the long-term changes in student performances that then correspond to their learning.

I asked my son a couple of weeks later if he thought 1/3 was equal to 3/4. He told me, “Oh no Daddy. 1/3 is definitely less than a half and 3/4 is definitely more than a half, so they can’t be the same.” As it turns out, the lesson in which he made the first statement was focused on being able to place fractions on a number line in order to be able to compare the relative size of different fractions. So he learned something about towards that objective, even though his performance during the lesson seems like he did not.

My colleague Liz created this graphic which nicely summarizes our project’s position on the relationship between conceptual understanding, procedural fluency, and application.

A typical week of teaching

The balance between conceptual understanding, procedural fluency, and application depends on your goals with your students and those goals should depend on what you know about your students. This is why I’m opposed to “Problem Solving Fridays” and “Practice Tuesdays” as these ways of deciding on goals over-simplify teaching to the detriment of student understanding.

In an age where we can provide instantaneous access to high-quality encyclopedias and generate customized user-generated-playlists for a billion people on the fly, we should be able to provide curriculum with more ambitious goals and more customizable content than what is currently provided to teachers. The typical curriculum resources teachers have access to today are not structured so that teachers will actually use them (1) and do not adequately support multiple pathways to support all students.

When I first started teaching, I was given a single sheet of paper by the district supervisor for mathematics with a list of twenty questions on it. He told me, “David, If you can get the kids to answer all of these problems by the end of the year, then you are set.” That was the entirety of the direction I was provided as a first year teacher in terms of curriculum and instruction. It took me weeks to find any textbooks in the school and I didn’t really learn what was on the end of year state assessment until I was scoring my students’ work on it. No first-year teacher should be provided so little direction and support.

Is this curriculum?

In my second year of teaching, I was given a textbook and a pacing guide and told that my job was to “cover the curriculum” and make sure that my students got the same experience as other students in other classrooms. I was told that if my supervisor came and observed me and I was not on pace, then I would be automatically given a poor evaluation.

Neither of these approaches to curriculum support works. Either teachers are expected to each individually recreate the wheel or they are treated as completely incapable of making curriculum choices. Teachers must both have sufficient guidance on what to teach and simultaneously the autonomy to adapt and extend curriculum resources to meet their students’ needs.

There is a mindset across many in the teaching profession that teachers should be both be designers and implementers of curriculum. However as Robert Pondiscio notes in his article, “How We Make Teaching Too Hard for Mere Mortals” (2), this leads to a lot of teachers using Google or Pinterest as a primary lesson planning resource which results in an incoherent experience for children. It also is more likely to lead to lessons where the task hasn’t been fully thought through and so any classroom discussions and potential learning opportunities that are embedded within the lesson are more likely to fall flat.

An example of a resource found via Pinterest (source)

Designing curriculum to support learning is a surprisingly challenging and time-consuming task. Suppose for example that you are designing curriculum for a unit on geometry at the elementary school level. It is highly likely that your curriculum will need to include, for example, pictures of triangles like these ones.

Two triangles in a typical curriculum

There are actually two issues with not being careful about how you use geometric representations with students. If every one of the triangles you draw has one side of the triangle parallel to the bottom of the piece of paper they are drawn on, then students may think that this is a property of triangles. If every triangle has somewhat similar length sides like the ones above then students may think that triangles that look longer and skinnier are not triangles. My own four year old son refers to long skinny triangles as lines, since these triangles have more in common, in his experience, with lines than with the shapes above he happily calls triangles.

Further curriculum is more useful when one lesson deliberately builds on the prior lessons. Teachers often focus on the day to day job of having things to do with students and rarely have the time to deliberately use what they have already done with students and build on their shared experiences. Some mathematical ideas are too big to contain within one lesson, and so planning day-to-day leads to an incoherent experience for children (3).

Curriculum has the potential to offer so much more than just resources for teachers to use in lessons. It can be a tool where they continue the learning about the content they teach that their education schools rarely have time to complete. Across the United States, many teachers now teach out of the content area for which they were trained, and so embedding opportunities to learn this content for teachers is especially important.

When the teachers’ manual, which usually contains somewhat repetitive suggestions for teaching, is only a click away from the resource a teacher is accessing, then learning about pedagogy can more easily be embedded within the curriculum. Deborah Ball is leading a project (4) to determine the highest leverage content (5) and pedagogy to be taught before teachers start teaching. What if curriculum authors were able to carry on this work with in-service teachers? What if the curriculum deliberately and explicitly offered multiple pathways through the curriculum?

One of the major areas I knew almost nothing about when I finished my degree in education was the ways students typically understand and misunderstand mathematics (6). In order to be best positioned to remediate common errors and misconceptions students make while learning mathematics, I need to know both strategies for this remediation and to know the ideas to be remediated. When you look across just the high school mathematics curriculum, the number of different ways students typically understand each mathematical idea varies greatly, and so the sheer amount of information about student understanding that a teacher would need to know is overwhelming. No one has successfully captured all of these ways of knowing yet, but some efforts exist, at least at the elementary school level (7). An ambitious curriculum would keep track of at least some of these common ways of understanding mathematics so that teachers who are planning units can reference these resources on demand.

A sample resource intended to address a misconception (source)

Further when I learned more about actively supporting students in developing productive dispositions towards the mathematics I taught, I learned that framing student ideas as either ‘knowing the math’ or as a misconception isn’t all that helpful. I now think of students as making sense of the world around them and try to figure out how their ideas are logical, given what the children know, rather than try to find the mistakes children make (8). What if the curriculum teachers accessed explicitly offered suggestions on how to improve students’ self-conceptions of themselves as mathematicians?

Teaching in response to what children know or do while working on authentic mathematics tasks (9) is difficult yet most curriculum resources offer almost no support for teachers in doing this. The most common understanding of formative assessment is that it is a type of assessment teachers give in order to determine what children know, but as Dylan Wiliam’s book Embedded Formative Assessment (10) shows, this is a limited definition and perhaps not helpful definition of formative assessment. Given the importance of formative assessment in teaching, strategies for formative assessment, like the 5 Practices for Orchestrating Productive Mathematics Discussions (11), could be embedded right into the planning materials for the curriculum.

Another major area of my own learning was about the use of mathematical representations to support student learning. I knew mathematics and I knew many mathematical representations of that mathematics, but I had not deliberately been exposed to mathematical representations, such as tape diagrams or area models, during my teacher training. An excellent curriculum would support teachers in making explicit connections between different representations and as a result, being better prepared to select mathematical representations to use with their students. Mathematical representations are an excellent tool for students (and their teachers) to make connections between different mathematical ideas and as such should be forefronted in curricular resources. Further, a cohesive curriculum should be written such that the representations that start their use early in a child’s school career make it easier for the same child to make mathematical connections in their future mathematics classes.

Sample representation (source)

When we can provide curriculum electronically, the resources that can be included for any given lesson or activity are limitless, yet we still design most curriculum with the limitations of print. A truly ambitious curriculum would have typical student approaches, useful mathematical representations, suggestions for pedagogy, specific tasks to support a mathematical idea, and other resources all within a click. Why not supply slides and templates for teachers to use so that teachers can focus on other more important aspects of their craft, such as anticipating student thinking for the upcoming lesson?

And it goes without saying that the strategic use of technology should be embedded within the curriculum with the caveat that given the current state of technology across the United States, that curricular resources should work in a variety of contexts. Some schools have one computer per classroom which might be hooked up to a projector, other schools have devices for each child; an ideal curriculum supports all likely arrangements of technology.

In Todd Rose’s The End of Average (12) he recounts a story about the design of the cockpit of an airplane, which I believe should inform curriculum writing:

…

After multiple inquiries ended with no answers, officials turned their attention to the design of the cockpit itself. Back in 1926, when the army was designing its first-ever cockpit, engineers had measured the physical dimensions of hundreds of male pilots (the possibility of female pilots was never a serious consideration), and used this data to standardize the dimensions of the cockpit. For the next three decades, the size and shape of the seat, the distance to the pedals and stick, the height of the windshield, even the shape of the flight helmets were all built to conform to the average dimensions of a 1926 pilot.

…

Out of 4,063 pilots, not a single airman fit within the average range on all 10 dimensions. One pilot might have a longer-than-average arm length, but a shorter-than-average leg length. Another pilot might have a big chest but small hips. Even more astonishing, Daniels discovered that if you picked out just three of the ten dimensions of size — say, neck circumference, thigh circumference and wrist circumference — less than 3.5 per cent of pilots would be average sized on all three dimensions. Daniels’s findings were clear and incontrovertible. There was no such thing as an average pilot. If you’ve designed a cockpit to fit the average pilot, you’ve actually designed it to fit no one.

The cockpit of an airplane (source)

What about curriculum? We all know that children enter classrooms in many different shapes and sizes, and that their understanding of the content we intend to teach is as varied, and yet we design curricular resources that mostly aim to support an average child. What if there is no such average child? The curriculum that aims to best support the average child may in fact support no one best.

It is well-known, for example, that students need multiple opportunities to both learn a mathematical idea and to access their memory of the idea in order to strengthen their memories (13). Almost no curricula deliberately interleave practice or offer opportunities for spaced retrieval practice. What if a curriculum deliberately included ideas from cognitive science into its construction?

There are also strategies for supporting students with special needs and emergent bilingual students which offer additional avenues for students to access the same mathematical content as their peers and which when implemented effectively, support all students. Many curricula offer no deliberate pedagogical suggestions for different populations of students, but in New York City alone there are more than 170,000 students with special needs and over 140,000 (14) students who are learning English as a second language. Given that access to education is a fundamental human right (15), our curriculum resources should offer the greatest possibility that all students have access rather than being a potential limiting factor.

One suggestion for this curriculum is to embed the use of instructional routines (16) throughout. In our work (17) on curriculum we have discovered that instructional routines offer support for teachers and students in multiple ways. Since they routinize the “steps” to a lesson in predictable ways, they allow teachers to focus on the parts of the lesson that change in response to the students and the mathematical ideas presented within the routine structure. Similarly, curriculum developers are able to develop tasks for instructional routines more rapidly and with more confidence that they will be used in the way intended when the possible ways the task will be enacted with children are more narrowly defined. Since students and teachers know what to expect next when the routine unfolds, they can more completely focus on each other and their mathematical reasoning. These routines also allow teachers to learn from their enactment as they “temporarily hold some [parts of their teaching] constant while working on others.” (18) Finally, well designed routines embed formative assessment into the structure of the routine (19) so that the challenging work of responsive teaching becomes more manageable to learn.

Finally, the license and formatting of curriculum resources should encourage both thoughtful revisions to the curriculum and the sharing of those revisions back to the greater community. In the United States, we have a million mathematics teachers, each basically writing lessons and altering resources on their own to support their students’ understanding, and no shared pool of resources from which to iterate. While online communities (20) have sprung up around different instructional routines, there is no policy in place nor organization that has stepped up to help organize those routines and their associated resources into a cohesive collection that can be built upon. Further, access to curricular resources is highly uneven across the many thousands of school districts across the United States, and a more open access model may help mitigate education inequities.

It is not likely that such an ambitious curriculum will emerge on its own. It will require the combined efforts of many hundreds of teachers and curriculum specialists working over a decade or two to design, test, and iterate to create a coherent collection of resources. Educational researchers should be included from the beginning of the curriculum construction so that they can rigorously test the impact of the curriculum on student learning. Professional development providers should be included so that the professional learning experiences of teachers who volunteer to be part of this effort can be aligned to the aims and beliefs about learning embedded within the curriculum structures.

Given that funding for education appears to be already stretched, this additional effort may need to be funded by outside partners. However the potential for such a project to have a long-lasting impact on student learning is great. We already know that curriculum impacts student learning (21); what might be the impact of an ambitious curriculum?

References:

1. Meyer, D. (2016). NCTM Puts Up a Sign, Retrieved from http://blog.mrmeyer.com/2016/nctm-puts-up-a-sign/ on September 6th, 2016.
2. Pondiscio, R. (2016), How We Make Teaching Too Hard for Mere Mortals, Retrieved from http://educationnext.org/how-we-make-teaching-too-hard-for-mere-mortals/ on September 6th, 2016.
3. Daro, P. (2013). Teaching Chapters, Not Lessons, Retrieved from https://vimeo.com/79909978 on September 6th, 2016
4. Ball, D. et al. (2013). Teaching Works, Retrieved from http://www.teachingworks.org on September 6th, 2016

5. Ball, D., Hill, H., and Bass, H. (2006), Knowing Mathematics for Teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, 29(1), p. 14-17, 20-22, 43-46., Retrieved from https://deepblue.lib.umich.edu/bitstream/handle/2027.42/65072/Ball_F05.pdf on September 6th, 2016

6. Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching what makes it special?. Journal of teacher education, 59(5), 389-407.
7. Carpenter, T., Fennema, E., Franke, M., L. Levi, and S. Empson. (2014) Children’s Mathematics, Second Edition: Cognitively Guided Instruction. Portsmouth, NH: Heinemann
8. Wees, D. (2015) Mistake Makers or Sense Makers. Retrieved from https://www.youtube.com/watch?v=1N10pp1GdXE on September 6th, 2016
9. Lampert, M., Beasley, H., Ghousseini, H., Kazemi, E., Franke, M. (2010) Using designed instructional activities to enable novices to manage ambitious mathematics teaching (pp. 129-141). In M.K. Stein & L. Kucan (Eds.) Instructional explanations in the discipline. New York: Springer.
10. Wiliam, D. (2011). Embedded Formative Assessment. Bloomington, Solution Tree.
11. Stein, M., Smith. M. (2009). 5 Practices for Orchestrating Productive Mathematics Discussions. Reston, VA. The National Council of Teachers of Mathematics
12. Rose, T. (2016) The End of Average. New York, Harper Collins.
13. Smith, M. and Weinstein, Y. (2016) Six Strategies for Effective Learning. Retrieved from http://www.learningscientists.org/blog/2016/8/18-1 on September 6th
14. Statistical Summaries. (2016), Retrieved from http://schools.nyc.gov/AboutUs/schools/data/stats/default.htm on September 6th, 2016
15. The Right to Education. (2016), Retrieved from http://www.unesco.org/new/en/right2education on September 6th, 2016
16. Lampert, M., Graziani, F. (2009). Instructional Activities as a Tool for Teachers’ and Teacher Educators’ Learning. Retrieved from http://tedd.org/wp-content/uploads/2014/11/Graziani-Lampert-Instructional-Activities.pdf on September 6th, 2016
17. A2i Project (2012 to 2016), see http://math.newvisions.org for resources and further details.
18. Lampert, M., Beasley, H., Ghousseini, H., Kazemi, E., Franke, M. (2010) Using designed instructional activities to enable novices to manage ambitious mathematics teaching (pp. 129-141). In M.K. Stein & L. Kucan (Eds.) Instructional explanations in the discipline. New York: Springer.
19. Wees, D. (2016). Instructional Routines As Formative Assessment. Retrieved from https://davidwees.com/content/instructional-routines-as-formative-assessment/ on September 6th.
20. Welcome to the Math Twitter Blogosphere. (2011), Retrieved from http://mathtwitterblogosphere.weebly.com/ on September 6th, 2016
21. What Works Clearinghouse, Interventions in Math, Retrieved from http://ies.ed.gov/ncee/wwc/FindWhatWorks.aspx?o=9&n=Mathematics/Science&r=1 on September 6th, 2016

Across the United States, there is a continued focus on the use of formative assessment to improve the conditions for students’ learning. One common theme is that teachers want more support in implementing formative assessment strategies in their classroom and that they want the use of formative assessment to be instructionally efficient.

What is formative assessment?

This is funny but it isn’t feedback that moves learning forward.

While formative assessment is defined very differently in different places, the framework I’ll assume for this article is the one proposed by Dylan Wiliam (Embedded Formative Assessment, 2011) wherein formative assessment is built up of five key strategies:

1.  Clarifying, sharing, and understanding learning intentions and criteria for success,
2.  Engineering effective classroom discussions, activities, and learning tasks that elicit evidence of learning,
3.  Providing feedback that moves learning forward,
4.  Activating learners as instructional resources for one another, and
5.  Activating learners as owners of their own learning.

Not only are there different definitions for formative assessment there are also different time-spans over which eliciting evidence of student achievement, a key aspect of formative assessment operates: over the course of a unit, day to day, or in the moment.

One very typical model of formative assessment involves school districts focusing on common unit assessments and common data tools in order to focus teachers’ attention on long-range planning in response to student performance data. Another shorter range focus is on modifying day to day lessons based on exit tickets and quizzes. However where formative assessment often falls short in terms of implementation is in the moment to moment decisions made by students and teachers in the classroom.

Further, much of what passes for formative assessment focuses on students making mistakes and teachers responding to those mistakes with corrective feedback. In many cases, choosing the feedback to give to students is time-consuming and actually ineffective. I propose that it is less important to focus on the mistakes that students make and more important to focus everyone’s attention, students included, on the reasoning that students do.

Instructional Routines as an answer

What would a routine that offers the rich features of formative assessment but allows teachers to be responsive in the moment look like? Can we design a routine which does not take an enormous amount of time for teachers to plan given the real time constraints faced by teachers? Can the instructional routine focus teachers and students more on understanding student reasoning rather than just identifying mistakes?

In their 2009 article entitled “Instructional Activities as a Tool for Teachers’ and Teacher Educators’ Learning,” Magdalene Lampert and Filippo Graziani introduced the idea of instructional activity for ambitious teaching. They define an instructional activity as “designs for interaction that organize classroom instruction”. Expanding on this definition to capture a distinction between instructional activities and instructional routines, instructional routines are “designs for interaction that organize classroom instruction”, shared amongst a group of teachers, that are repeated using different content and goals, frequently enough that both teachers and students can internalize the structure of the lesson.

These instructional routines could become a standard way of working that every other profession, aside from teaching, has developed to standardize and professionalize their work. I offer that these instructional routines are also the rich formative assessment-embedded activities that we have all been waiting for.

The greatest benefit of these instructional routines is their routine-ness. Instead of having to invent a different lesson plan or activity for every different mathematical idea, a teacher can select an instructional routine appropriate to the mathematics at task. Rather than having to re-invent teaching each day, planning teaching becomes more about choosing mathematical goals, selecting tasks to support those goals, and then embedding these tasks within an activity.

But why are these instructional routines useful for formative assessment? Let’s look at one instructional routine, Contemplate then Calculate, to see how it aligns with Dylan Wiliam’s definition of formative assessment introduced earlier. (Here are other examples of instructional routines)

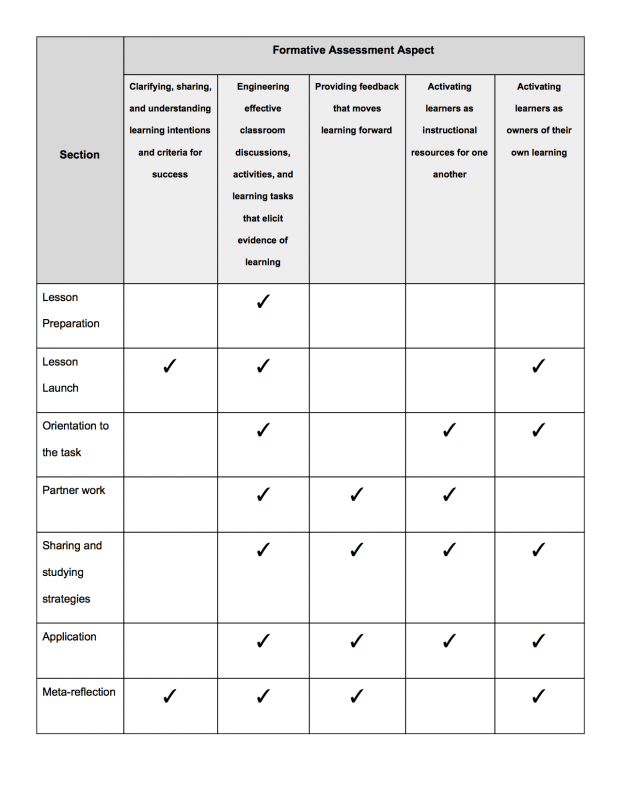
Elements of Formative Assessment in Instructional Routines (click to view larger)

Here are some key elements that teachers need to consider when implementing instructional routines in their classrooms and their relationship to formative assessment.

Lesson preparation

In enacting this kind of instructional routine, a teacher needs to select a mathematical problem, ideally one rich enough for students to have something to talk about and one that will focus students on a particular mathematical goal. Once a task is selected, in order to make the best use of the instructional time with their students, this teacher anticipates the different approaches her students might make.

For example the task selected might ask students to identify the number of white squares in the following image without counting all of them. In this case, the goal is to support students using mathematical structure (Common Core Math Practice 7) to identify ways of chunking the figure in order to make it easier to work with and to allow students to connect what they know about multiplication to counting squares. (Here are more sample tasks, each of which could be the mathematics that is inserted into the instructional routine).

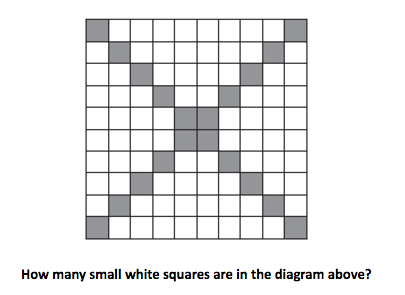
Before giving the task to students, it is useful to anticipate strategies students might use. For this task, one potential strategy is to chunk the diagram and notice that there are four identical triangle-like shapes. One can then zoom into one of these triangles to see that it is formed of four rows, each of which is two squares longer than the row above it, so since we start with two in the first row, the triangle-like shape has 2 + 4 + 6 + 8 = 20 total white squares for one triangle-like shape. Since there are four of these shapes, there are 20 × 4 = 80 total small white squares.

By identifying potential strategies in advance, the teacher is better equipped to circulate around the classroom during the portion of an instructional routine where students are working together and listen to student conversations and observe them work. During the portion of an instructional activity where students are presenting their ideas, anticipating strategies makes it easier for the teacher to focus students on a particular mathematical goal and make the mathematics evident in the solution explicit for everyone through careful annotation.

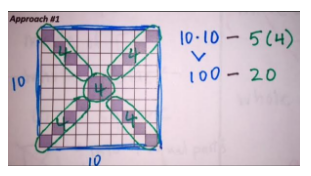
Here is an example of three annotations and three descriptions of student strategies. Which annotation goes with which strategy? How do you know?

Approach #1

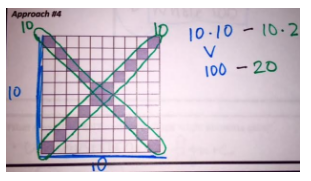
Approach #2

Approach #3

Description 1

“I chunked the shape into four triangle-like shapes and counted the number of squares in each row, and then multiplied this by four.”

Description 2

“I noticed five groups of four grey squares, which is 20 squares and I subtracted that from the big 10 by10 square to get the remaining white squares.”

Description 3

“I noticed that each row has 2 grey squares, so there are 20 grey squares because there are 10 rows. I then subtracted these from the big 10 by 10 square.”

By deciding in advance on various ways to annotate the task when students describe their strategies, teachers can shift their cognitive load while teaching from remembering what they want to say next to really listening to what students are saying and support other students in the class in doing the same.

The Parts of One Instructional Routine: Contemplate then Calculate

Lesson launch

This instructional routine starts with a launch designed to make it more likely that students understand both the purpose of the activity and their role within the activity. This script allows students to orient toward the goal themselves and aligns most directly with ‘clarifying the learning intentions’ formative assessment strategy. The meta-reflection activity at the end of the instructional activities helps students see progress towards those goals themselves as well.

Orientation to the task

Students are then given an independent opportunity to notice key features of a problem, followed by time with a partner to share what each noticed and briefly discuss how that could be mathematically useful. During this time, the their teacher circulates around the room and gathers information on what students are thinking about. Students are then gathered together for a whole classroom sharing of the mathematical structures, patterns, and/or quantities noticed. The teacher records these noticings so that they become the shared knowledge of all the students in the classroom. Because the cognitive demand of “notice” is relatively low, all students can participate in this orientation; because the noticings are shared, all students develop ownership of the task–long before any struggles would prevent their investment.

Partner work

Next, students use the gathered information to build and share a solution strategy while teachers have amply opportunity to circulate around the classroom and listen to what students think and use this as evidence of what they understand and more importantly, how they understand it. Since each instructional activity includes preparation work ahead of time where teachers anticipate the kind of thinking they expect, teachers are now better able to contrast their expectations of student thinking against the actual live student thinking they encounter.

By working within a structured routine, students also have less extraneous information to pay attention to in the mathematics classroom and are expending less of their total cognitive load on remembering what’s happening next and what their role is now; therefore, they are better equipped to pay attention to each other and to the mathematical ideas surfacing in the classroom. When students are able to pay closer attention to how each shared mathematical idea works, students get better feedback about their own ideas. Both of these observations are also true for teachers.

Sharing and studying strategies

Now the teacher orchestrates a whole class discussion around the mathematical focus for the day. The objective here is to use the thinking students have done and explicitly make this thinking public for everyone to understand by probing students for more detail, asking students to listen to and restate each other’s ideas . As a group, the role of students is to work as mathematicians do, by constructing and assessing arguments for the validity of their mathematical approaches and looking for connections between the various ways the class solved the problem for today.

During the partner work and sharing out portions of the activity, students are oriented not to the teacher’s talk but to each other’s speaking and thinking, which activates them as resources for each other. When the strategies conjectured by students are unpacked and made explicit for students through gesturing, annotation, and restatement, students can make clear sense of what mathematics is being discussed and why it works (or in some cases, why it does not work).

Meta-reflection

Since the goal of mathematics classes is not to learn how to solve individual problems, but to use problems to learn mathematical ideas, many of the instructional activities include a meta-reflection portion of the activity. Here students respond to a prompt or write about what they learned during the lesson. Ideally students should be able to describe what they learned in relation to the goal articulated at the beginning of the lesson.

Conclusion

“Instructional routines support teachers in studying the impact of teaching practice on student learning by focusing attention on the outcomes of a small, well defined, common set of practices that are repeated for a given period of time.” (Deeper Learning, Magdalene Lampert, 2015) The goal of these activities is to allow teachers to better study their own impact and to allow students to better see their progress in learning mathematics over time–to see themselves as doers of mathematics. Simultaneously, the same features that make instructional routines useful tools for developing teacher practice support teachers in integrating formative assessment practices as part of their teaching.

Formative assessment is not an exit ticket at the end of a lesson or a quiz every Friday. It is a framework for teaching and as such an instructional routine which aligns well to the framework is more likely to be useful for teaching than any attempt to layer formative assessment strategies on top of an existing set of routines.

In 1965 a pair of researchers, Robert Rosenthal and Lenore Jacobson, set out to study the Pygmalion Effect, which hypothesizes that if we hold high expectations for people’s performance, their performance will be better than if we hold low expectations.

Rosenthal & Jacobson, 1968

What they found was startling, especially for younger kids. Students who had been randomly selected as being likely to show potential based on an imaginary test and then this information communicated to their teachers, showed tremendous gains in the intellectual ability compared to the control group.

Rosenthal and Jacobson, 1968

The reverse effect, called the Golem Effect, has also found to have an impact through randomized-control-sample experimental design. This means that one factor into student performance is the expectations teachers have, either high or low, on that student performance.

Every time you refer to your students as “low kids” you are re-enforcing expectations of future achievement that limit children. #NCSM16

— David Wees (@davidwees) April 12, 2016

This is why I get incredibly frustrated when teachers use labels like “high” or “low” to describe their students. Invariably these labels are like self-fulfilling prophesies that lead to strengthening or weakening student beliefs about their own ability to be successful and lead to teachers, subconsciously, taking actions that lead to either higher or lower student performance, and as performance is related to student learning, this can be devastating.

Of course, this pernicious labeling of students is built right into our systems of education so we can hardly consider individual teachers to be at fault. We have the ELL students, the SpEd students, the “lower third”, the students who only achieved a 1 or a 2 on the NY state exam, the students who failed algebra last semester, and other unhelpful labels for students ad nauseam.

So what do we do? I propose a good starting place is to eliminate unhelpful labels from our own vocabulary. Another step is to talk to our colleagues about our shared use of labels for students. Find ways to look for and talk about strengths in students rather than perceived deficits.