Month: May 2015 (page 1 of 1)

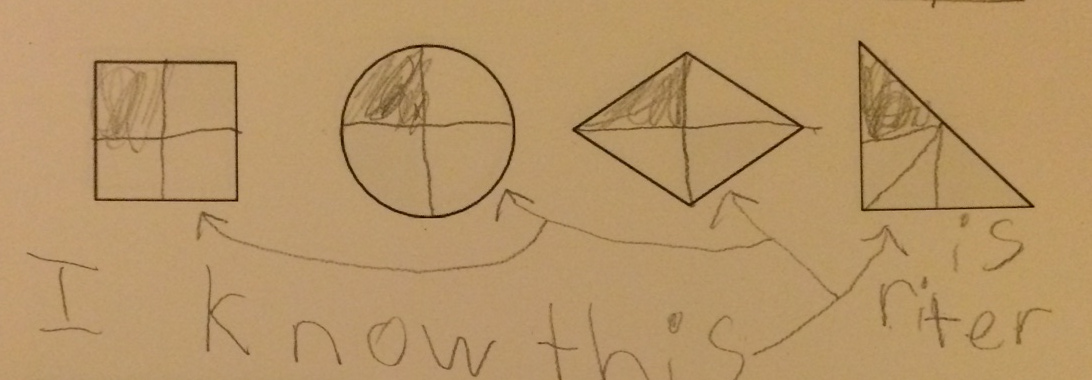
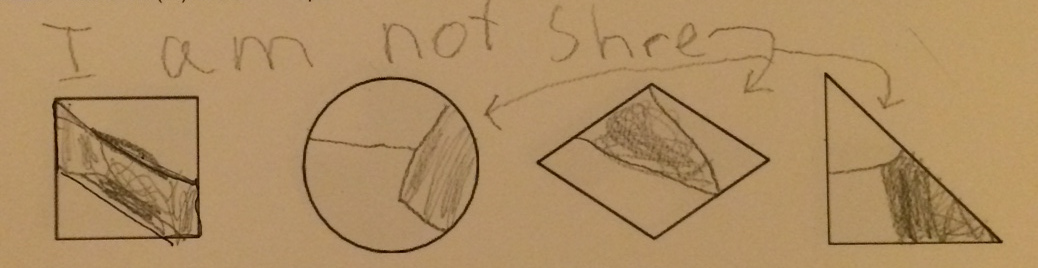
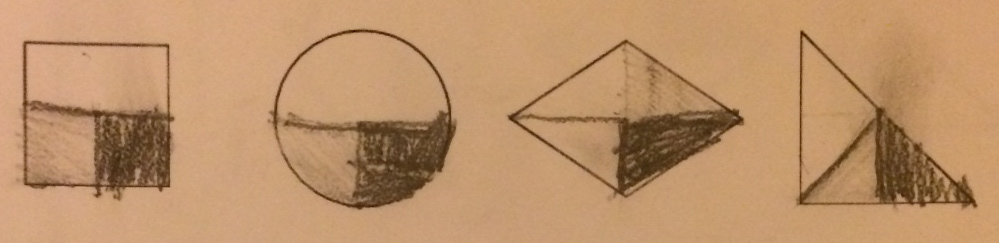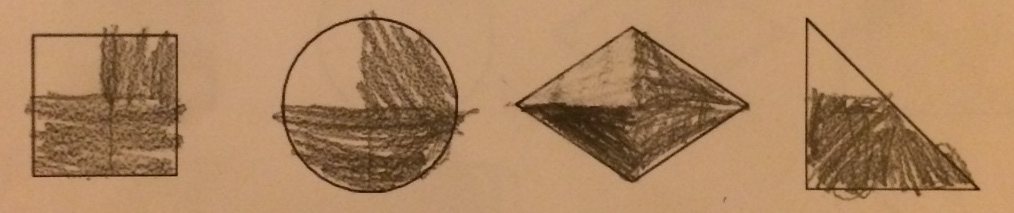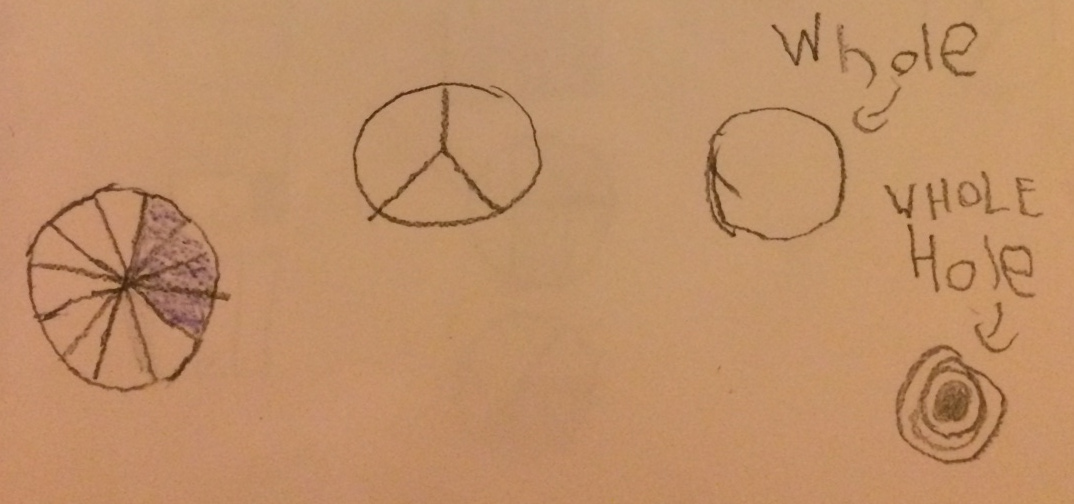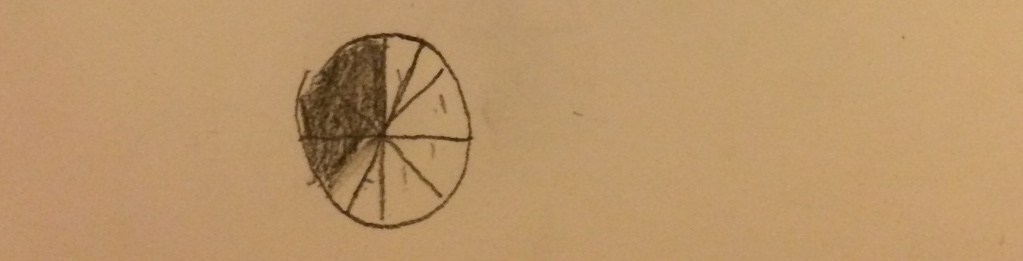This video is a brief demonstration, about 15 minutes, of some teaching I did at the 2015 New Jersey Association of Mathematics Teacher Educator meeting.

Unfortunately, the video tracking is not great so much of the annotation I was doing of the participant ideas is not easy to see as I am doing it.

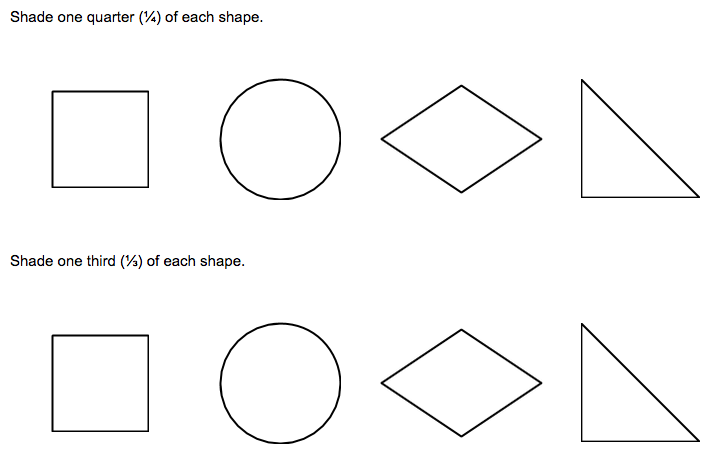
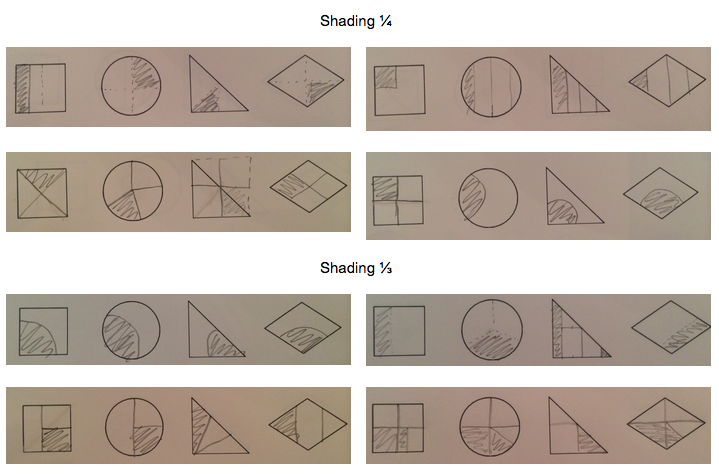
The instructional activity itself is called Contemplate, then Calculate and was developed by Grace Kelemanik and Amy Lucenta. The slides, script, resources, and references are available here.

Things I would do differently:

• Set up the projector screen in advance of starting the activity so I don’t have to fiddle with it during the strategy sharing.
• Not wing the recording of noticings and strategies because I ran out of time to prepare before this talk, but take the time to make a template for collecting data.
• Record the initial noticings of participants about the problem as they were happening.
• Bring my own markers so that I can ensure I have access to more than one colour when recording the student ideas.

Things I decided to do or not to do somewhat deliberately:

• I did not focus on student to student discourse during the full group portions mostly in the interest of time. My meta-objective for this activity was to share the overall structure in a somewhat limited amount of time.
• I did not enforce participants writing using the prompts mostly because I knew I had little to no relationships with participants and I wanted to make sure no one felt alienated during this portion of the talk.
• I did make sure that when I was recording student strategies that I tried not to impose, as much as I could, much interpretation of those strategies. One of the participants actually came up after-ward and said she really noticed that I was making an effort to write down representations of what participants were saying rather than filling in too many of the gaps based on my understanding of the problem.
• I also focused on having participants share multiple strategies to solving this problem rather than attempting to focus participants on seeing one particular strategy.
• I decided to summarize participant ideas at the end rather than take the time to have them share out to the room, mostly in the interest of time.

What else about what I did do you have questions or feedback about?

This is a recording of a keynote I gave at the New Jersey Association of Mathematics Teacher Educator (NJAMTE) annual meeting.

The audio isn’t terrific unfortunately but it is manageable. The slides, script, references, and resources are available here.

Fractions are hard. Of course, I knew this before my lesson on Saturday, but the responses of my students to a task really drilled that point home for me.

Here is the activity I gave my students to do:

Here’s what I anticipated they might do:

Here’s a sample of what they actually did:

Student 1

This student seems to understand that if you want to shade 1/4 of something, you want to split it into four equal parts and then shade one of those parts. The triangle drawn is more challenging to divide, so the student likely estimated their partitioning of it.

However, if one wants to shade 1/3 of an object, it looks like this student thinks that they need to split the shape into four unequal parts and shade the smallest of those parts, maybe because they think that 1/3 is smaller than 1/4?

Student 2

This student told me that they know that 1/4 is the same as “half of a half” and so they divided each of the shapes in half, and then divided one of those halves into a further half, and then shaded it.

When it came to shading 1/3 of a shape though, this student looks like they divided the shape into four equal parts and then shaded three of those parts. My guess is that they thought that fractions involve dividing into four parts, and then used the denominator of the fraction to choose how much to shade? I’m not sure that they noticed the inconsistency in this procedure and what they did in the first part.

Student 3

This last student seems to have done pretty much the same as the second student, but seems aware that when you want to shade 1/3 of a shape, you want to first divide it into three equal parts and then shade one of those parts. I asked them about it and they said they just weren’t sure how to cut the shapes into three equal parts.

With this gap between what I was expecting to see and what I actually saw, I was left without knowing an effective way to respond. I decided that this task had little entry points for someone who really did not know what 1/4 and 1/3 meant (one of my student’s work was blank, which I am not showing since I do not have permission).

With the worry in the back of my head that I was probably reducing the cognitive demand for students, we split into two groups with my student-teacher leading one group and me leading the other group and we tried a different task, one which offered some context through which one might make sense of what 1/3 means.

“If you had a pizza and you wanted to share it equally with three people, how would you cut it up so that each person got 1/3 of the pizza?”

With this prompt, students in my group almost all produced work similar to the following:

With one student drawing this:

This second student, by the way, said that pizza comes cut into ten-slices and so the best we could hope to do is to give each person 3 slices of the 10 and then give away the last slice to someone else.

The knowledge that would have helped me better anticipate student understandings here is what I call “the ways children typically understand mathematical ideas” and is the kind of knowledge that is rarely explicitly taught before starting teaching. Every time I teach a new topic, I notice that the ways students think about the ideas are different than what I expect, and over time, I learn to anticipate student thinking better as I get feedback from working with them.

If you had students showing these kinds of responses to this task, what would you do during your next lesson on fractions to support them?