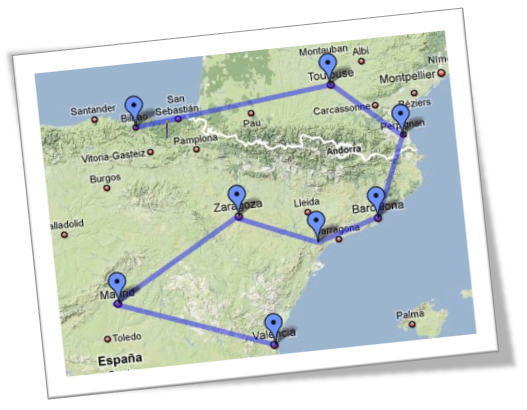
 I recently had students do a project where they apply the distance formula to finding the shortest path for a traveling salesperson to travel between 8 cities. The basic idea is, the students use the longitude and latitude coordinates as substitutes for the x and y coordinates of the city, then they can use the distance formula to find a pseudo-distance between the cities. Of course, on any kind of largish scale, this makes no sense, but on a small enough geographic scale the error in the distances is small, and I made sure the kids were aware of this deliberate error. This project was intended to be a chance for the students to get lots of practice using the distance formula.
I recently had students do a project where they apply the distance formula to finding the shortest path for a traveling salesperson to travel between 8 cities. The basic idea is, the students use the longitude and latitude coordinates as substitutes for the x and y coordinates of the city, then they can use the distance formula to find a pseudo-distance between the cities. Of course, on any kind of largish scale, this makes no sense, but on a small enough geographic scale the error in the distances is small, and I made sure the kids were aware of this deliberate error. This project was intended to be a chance for the students to get lots of practice using the distance formula.
You can view a sample of the students work here which I have permission from the student to share. This was rather an exceptional sample for many reasons. The first reason is that the student went to extraordinary measures to format his document and arrange his work in a clear logical sequence. Another reason I really enjoyed looking at this student’s project was because he had obviously done research about the traveling salesperson problem, including appropriate mathematical terminology such as the ‘Hamiltonian path’. He talks about the limitations of the approach we took, the errors he found in the project, and suggests an improved method than the brute force solution. He uses technological tools to his advantage, learning a bit of JavaScript to find the coordinates of the cities, and using Excel to greatly reduce his calculation time for the distances between the cities.
If all of our students work was so neatly arranged and so carefully done, I think very soon we’d soon have much different jobs. Instead of ‘instructing our students’ we would be learning from them as equal partners. This what I strive for in my teaching.