David Wees
University of British Columbia
(Download a copy of it here)
Abstract
The objective of this paper is to show that the costs of using educational technology are more than compensated by the savings schools can receive, provided the technology is introduced and used in the correct way. So many schools are looking to trim money from their budgets, and this paper aims to show some of the ways this can be done. The essential thesis is that productivity improvements will be where the majority of the savings will come from, with the remainder coming from conversion of the "old way" of doing things into the new cheaper technological method.
Introduction
Schools today, as always, are looking for ways to reduce costs. The current economic crisis and the recession of 2008 have hurt schools severely (Ring, 2008 & Tang, 2008) resulting in further cuts. This recession has impacted both public and private schools. Public schools rely on funds from taxes, which are always reduced in a recession since there is less income to tax. Private schools generally see enrollment drop during a recession as parents of their students lose their jobs due to the economic slow-down.
There are a few areas that schools can save money. Some schools cut services offered by the school, including dropping whole departments if necessary. Art and Music programs are disappearing all over North America as a result of the economic crisis and the No Child Left Behind law (Hetland & Winner, 2007).. Extra support services are also being removed from schools as school districts use "centralization" and "school sharing" as ways of reducing the hours school support staff are available at schools.
Technology has for many years been a focus of many schools. My current employment depends a lot on my talent with technology, in fact it is probably one of the primary reasons I was hired. This focus has probably developed as schools become more aware of the importance of what happens in a classroom reflecting what is happening in the real world. Without relevance to the real world, schools lose their value and certainly technology use is a huge focus of today’s world.
One of the ways that school can save money is by re-evaluating their current use of technology. Much of the money which is spent on educational technology is spent unwisely, with little thought given to the training technology requires or how the technology will actually be used.
A consistent trend in schools is that the way teachers teach changes as the schools adopt more current technology. Although schools are seen as resistant to change, over the years the opposite has been seen (Cuban, 1986). Schools have seen the introduction of radio, chalk boards, television, overhead projectors, internet, LCD projectors, interactive white boards, and most recently, mobile devices such as cell phones. Each of these devices comes with a cost which the school has to bear but has been shown to improve the education of the students within the school (Schacter, 1999).
There are many costs associated with this technology, some of which are purchase costs and can often be included as capital assets and others which are yearly costs and must be budgeted for each year. These costs can generally be categorized as either a hardware-related cost, or a training cost.
As computer hardware gets older, the cost to maintain the hardware increases. "A recent Gartner Group survey indicates IT budgets of companies worldwide amount to slightly more than 3.5% of revenue" (David, et al. 2002). Given that school board budgets, and even some school budgets, are usually in the millions of dollars, this cost is not insignificant. David, Schuff, and St. Louis (2002) describe how centralization and standardization can shave as much as 27% off of this maintenance cost.
In order to be able to do the standardization and centralization required to cut costs on IT, schools should have an expert on staff. Since the use of IT in education requires special considerations, this person should be both an expert in technology and an educator. The role of this person can also be to train staff in how to use this technology appropriately, which will save costs on hiring expensive educational consultants. As this person will be an integral part of the staff, they may be able to offset the “expert” phenomena, wherein teachers typically defer to the experts rather than learning the skills being taught themselves.
Another important observation to make is that cloud computing, in which information is stored on offsite servers and accessed through a web browser, can also greatly reduce costs for schools. Instead of paying for the cost of an onsite server and for maintenance of this server, one can run an entire school network offsite using cloud applications. One could use free cloud applications and replace almost all desktop software, saving an enormous of money in expensive licensing costs.
The cost of training staff how to properly use educational technology is not insignificant. One option is to send staff to regular technology training sessions, but many teachers will likely not continue to use skills they have learned unless they have on site support. With the recent improvements to e-training, it is also possible to train teachers externally without sending them to training sessions, saving on costs of transportation. Another option is have on staff a full time or part time technology expert whose role it is to provide on the job training for staff.
Note that, as David, Schuff and St. Louis mention, this centralization will not cut much cost off of the software licenses schools must purchase. These licenses are typically tied to either the number of devices running the software, or more often, to the number of users of the software. One way to cut a lot of costs in this area is to explore the use of open source alternatives to the expensive software packages schools usually purchase. From this author’s experience, although there are costs associated with running open source software, the free nature of the software means that these are quite often a lot less than what one would pay for proprietary software.
A typical school in the UK makes about 8,000 photocopies per student at a total yearly cost of £100,000 per school (Spencer, 2008). Given that Canadian education and UK education are not so different, we would expect to find similar costs for photocopying here as well. If a school were to use educational technology to move to paperless, they would save this cost (at least in paper) every year. The amount of time it takes to distribute electronic versions of resources to students is approximately the same as it is to distribute paper copies of resources.
With improved communication between faculty members and between students and faculty members some of the benefits are decreased costs due to fewer meetings. For example, Google Documents can be collaboratively edited and shared among staff. Time that was previously spent meeting to discuss the formation of documents, a frequent occurrence in this educator’s experience, can now be spent on more productive pursuits. For example more staff training, which is always difficult to time and pay for, can happen during what used to be meeting time.
Video conferencing has been used by many organizations as a way to save money. Cisco saved more than $100 million in travel and business expenses by switching much of their customer relations to video conferencing using their own technology (Manyika, Sprague, Yee 2009). Instead of sending educators to training sessions abroad and spending a fortune on travel expenses, schools could collaborate and create virtually cost-free webinar training sessions. Smaller schools could band together and use video conferencing to increase their course offerings, by allowing one teacher to serve more than one classroom simultaneously.
One of the areas where a lot of time is spent as a teacher is on administrative matters. Teachers have to keep track of attendance every class, record grades for every student, manage parent contacts, organize and maintain curriculum, and calculate their class budgets. There are free online tools such as School Tool which can be used to reduce the amount of time teachers spend on these tasks.
If one is careful about the use of proprietary tools, and manages the school’s technology wisely, money can be saved. In the switch from the Microsoft Outlook email system to Google’s Gmail for its 1800 employees; one construction company saw a cost savings of nearly $2 million which is a savings of nearly $1000 per employee (Lynch, 2008). The largest part of these savings was the removal of the necessity to manage their own email servers. Schools could see similar savings per student, especially not-for-profit schools for whom the Google Education accounts are free.
Similar savings can be seen elsewhere in the school. In an interview with Chris Franzen (personal communication, December 5th, 2009), a technology coordinator at a state-funded public school, he mentioned that one of the ways his school saves money is through the use of virtual field trips. Although we can all agree that a ‘live’ field trip is preferable to an electronic field trip, the costs of such trips can be quite prohibitive, especially once the cost of teacher coverage, transportation, site visits, and other miscellaneous costs are included.
"Nearly half of the high school dropouts point to boredom and lack of interest in classes as a reason for leaving school." (Kolderie, T., McDonald & Tim 2009) Increased engagement in school caused by meaningful lessons will lead to increased graduation rates which will lead to cost benefits for society. – "1 in 3 high school students in the Class of 2006 will not graduate this year ", (Kolderie & McDonald, 2009). Another article suggests that 82% of people in prison are high school drop-outs (Christle, Jolivette, & Nelson, 2007). Over the course of a decade the cost to the US taxpayer for dropouts is $3 trillion (Alliance for Excellent Education, 2009).
Given the opportunity to use technology meaningfully in school, students are more likely to remain in school. According to Gloucestershire College representative Perry Perrot (Coughlan, 2009) the use of Facebook in the school has increased student retention rates in their courses. He suggests that this is due to a ‘positive effect on [student] motivation’ and the comfort students feel using the social networking platform. Other examples of this phenomenon are easy to find, and many schools have opened up across North America which include technology as a focus. Not surprisingly, these schools often have lower drop-out rates than their comparable neighbourhood schools.
There are several places where schools can save money on both the cost to implement technology and the cost to run the schools themselves. Schools need to be willing to rethink the ways information in the school is transmitted and shared and develop the flexibility to use new tools where necessary.
Much of the cost savings described here have been developed in the past 5 years. At our current rate of technological advance, every two years our knowledge about technology doubles. Without an expert on staff to keep the school abreast of changes and best practices in technology use, schools will quickly become obsolete. With obsolescence comes increased costs to maintain equipment and upgrade software, as well as compete with other local schools who have kept their technological skills up to date.
Predicting the future has become increasingly difficult given the rapid rate of knowledge acquisition. We cannot now predict what jobs will exist when our current high school students graduate university, but it seems likely that they will require technical expertise given current trends in job development. Without the training in technology that secondary schools offer, the cost to train our students will have to borne by either the future employers of our students, or by society.
Although there is some resistance in education to following business models, it seems clear that what many businesses are doing to save money would work in schools. As previously stated businesses are centralizing their services, standardizing their use of IT in multiple locations and developing innovative ways to use technology. Schools would do well to observe the practices businesses follow.
The factory model of education based on how businesses operate does not work because not all children are the same. Fortunately new models of education are replacing the factory model (Matusov, Rogoff, and White 1996) where the learners have much more control over their learning.
Technology definitely helps make this learner centered learning much easier as it provides tools for student collaboration and creation. Although the expense of educational technology can be great, creative school administrators and technology coordinators can still find ways to reduce operating costs using technology.
References
Ash, K. (2009), ‘Experts Debate Cost Savings of Virtual Education’, Education Week 28(25).
Chaddock,G.R.,(2006), US High School Dropout Rate: High, But How High? The Christian Science Monitor, June 21, 2006, retrieved from www.csmonitor.com/2006/0621/p03s02-ussc.html on November 18th, 2009.
Christle, C., Jolivette, K., & Nelson, C. (2007). School Characteristics Related to High School Dropout Rates. Remedial and Special Education, 28(6), 325-339.
Coughlan, S., (2009) Facebook ‘cuts studnt drop-outs’, http://news.bbc.co.uk/2/hi/uk_news/education/8299050.stm, retrieved on December 6th, 2009
Cuban, L. (1986). Teachers and Machines: The Classroom Use of Technology since the 1920s, retrieved from http://www.csun.edu/~jnk61575/sed514/docs/cuban_intro.pdf on December 5th, 2009
David, J.S., Schuff, D., St. Louis, R., (2002), Managing your IT Total Cost of Ownership, ACM 0002-0782/02/0100, retrieved from http://portal.acm.org/citation.cfm?id=502273 on December 5th, 2009
Du Vivier, E. (2008), ‘Costs and Financing in Open Schools’, Commonwealth of Learning , Commonwealth of Learning. 1055 West Hastings Suite 1200, Vancouver BC V6E 2E9, Canada. Tel: 604-775-8200; Fax: 604-775-8210; e-mail: info@col.org; Web site: http://www.col.org
Dunleavy, M.; Dexter, S. & Heinecke, W. F. (2007), ‘What Added Value Does a 1:1 Student to Laptop Ratio Bring to Technology-Supported Teaching and Learning?’, Journal of Computer Assisted Learning 23(5), 440–452.
Guhlin, M. (2007), ‘The Case for Open Source: Open Source Has Made Significant Leaps in Recent Years. What Does It Have to Offer Education?’, Technology & Learning 27(7), 16.
Hetland, L., Winner, E. (2007). Arts for Our Sake. School Arts Classes Matter More Ever – But Not for the Reasons You Might Think. The Boston Globe, retrieved from http://www.fultonschools.org/k12/Art/documents/ArtForOurSake.pdf on July 23, 2010
Kolderie, T.; McDonald & Tim (2009), ‘How Information Technology Can Enable 21st Century Schools’, Information Technology and Innovation Foundation , Information Technology and Innovation Foundation. 1101 K Street NW Suite 610, Washington, DC 20005. Tel: 202-449-1351; Fax: 202-638-4922; e-mail: mail@itif.org; Web site: http://www.itif.org
Lynch, C.G., (2008), Cost Savings Found When Microsoft Outlook Ousted for Gmail at British Construction Firm, retrieved from http://www.cio.com/article/429863/Cost_Savings_Found_When_Microsoft_Outlook_Ou sted_for_Gmail_at_British_Construction_Firm_ on December 6th, 2009
Manyika, J., Sprague, K., Yee, L., (2009) Using Technology to Improve Workforce Collaboration, retrieved from http://whatmatters.mckinseydigital.com/internet/using- technology-to-improve-workforce-collaboration on December 6th, 2009
Matusov, E., Rogoff, B., White, C., (1996). Models of Teaching and Learning: Participation in a Community of Learners, retrieved from http://ematusov.soe.udel.edu/vita/Articles/Rogoff, Matusov, White, Models of Teaching, 1996.pdf on December 6th, 2009
McIntire, T. (2006), ‘Enough to Go ‘Round? Thinking Smart about Total Cost of Ownership’, Technology & Learning 26(12), 20.
Morrison, J. (2003) U.S. Higher Education in Transition, On the Horizon, 11(1), pp. 6-10. Retrieved from http://horizon.unc.edu/courses/papers/InTransition.html
Nadeau, B. (2008), ‘Keeping VoIP from Being the Wrong Number: Digital Phones Can Save Money for Schools but There Are Many Pitfalls’, Technology & Learning 29(4), 31.
Salpeter, J. (2009), ‘Textbook Deathwatch’, Tech & Learning 30(1), 26.
Schacter, J., (1999). The Impact of Educational Technology on Student Achievement: What the Most Current Research Has to Say, retrieved from http://www.waynecountyschools.org/150820127152538360/lib/150820127152538360/im pact_on_student_achievement.pdf on December 5th, 2009
Spencer, J., (2008). Can we give every school child in the UK a Linux notebook and still save money? retrieved from http://www.computerworlduk.com/community/blogs/index.cfm?entryid=951&blogid=17 on December 7th, 2009
Ring, S. (2008). The Edutopia Poll. Edutopia, retrieved from http://www.edutopia.org/poll-financial-crisis-school-impact on July 23, 2010
Tang, A. (2008). Economic Crisis Hits Schools. Our Education, retrieved from http://blog.oured.org/2008/10/economic_crisis_hits_schools.php on July 23rd, 2010
The High Cost of High School Dropouts: What the Nation Pays for Inadequate High Schools (2007), Alliance for Excellent Education, retrieved from http://www.adlit.org/article/19706 on November 18th, 2009
Tucker, B. (2009), ‘Florida’s Online Option’, Education Next 9(3), 12–18.
Villano, M. (2006), ‘The Road to Paperless’, Campus Technology 20(3), 40–42.
Witkowsky, K. (2008), ‘Increasing Learning and Reducing Costs through Technology: The University of Alabama Story’, Change: The Magazine of Higher Learning 40(2), 32–38.
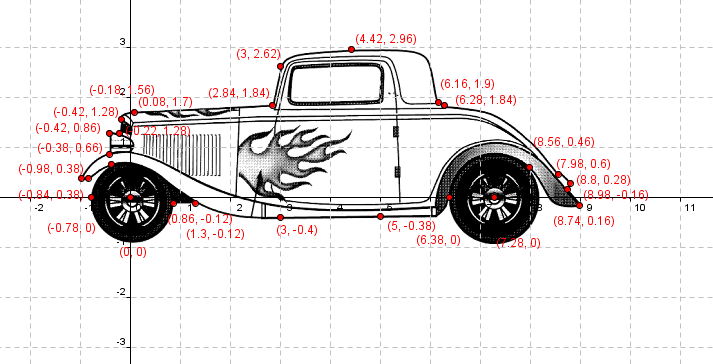
 I recently had students do a project where they apply the distance formula to finding the shortest path for a traveling salesperson to travel between 8 cities. The basic idea is, the students use the longitude and latitude coordinates as substitutes for the x and y coordinates of the city, then they can use the distance formula to find a pseudo-distance between the cities. Of course, on any kind of largish scale, this makes no sense, but on a small enough geographic scale the error in the distances is small, and I made sure the kids were aware of this deliberate error. This project was intended to be a chance for the students to get lots of practice using the distance formula.
I recently had students do a project where they apply the distance formula to finding the shortest path for a traveling salesperson to travel between 8 cities. The basic idea is, the students use the longitude and latitude coordinates as substitutes for the x and y coordinates of the city, then they can use the distance formula to find a pseudo-distance between the cities. Of course, on any kind of largish scale, this makes no sense, but on a small enough geographic scale the error in the distances is small, and I made sure the kids were aware of this deliberate error. This project was intended to be a chance for the students to get lots of practice using the distance formula.