Across the United States, there is a continued focus on the use of formative assessment to improve the conditions for students’ learning. One common theme is that teachers want more support in implementing formative assessment strategies in their classroom and that they want the use of formative assessment to be instructionally efficient.
What is formative assessment?

This is funny but it isn’t feedback that moves learning forward.
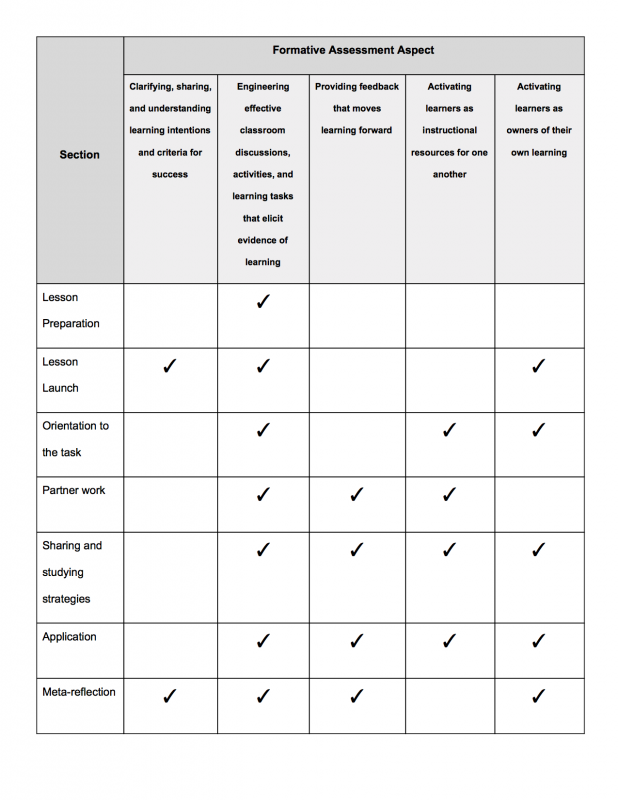
While formative assessment is defined very differently in different places, the framework I’ll assume for this article is the one proposed by Dylan Wiliam (Embedded Formative Assessment, 2011) wherein formative assessment is built up of five key strategies:
1. Clarifying, sharing, and understanding learning intentions and criteria for success,
2. Engineering effective classroom discussions, activities, and learning tasks that elicit evidence of learning,
3. Providing feedback that moves learning forward,
4. Activating learners as instructional resources for one another, and
5. Activating learners as owners of their own learning.
Not only are there different definitions for formative assessment there are also different time-spans over which eliciting evidence of student achievement, a key aspect of formative assessment operates: over the course of a unit, day to day, or in the moment.
One very typical model of formative assessment involves school districts focusing on common unit assessments and common data tools in order to focus teachers’ attention on long-range planning in response to student performance data. Another shorter range focus is on modifying day to day lessons based on exit tickets and quizzes. However where formative assessment often falls short in terms of implementation is in the moment to moment decisions made by students and teachers in the classroom.
Further, much of what passes for formative assessment focuses on students making mistakes and teachers responding to those mistakes with corrective feedback. In many cases, choosing the feedback to give to students is time-consuming and actually ineffective. I propose that it is less important to focus on the mistakes that students make and more important to focus everyone’s attention, students included, on the reasoning that students do.
Instructional Routines as an answer
What would a routine that offers the rich features of formative assessment but allows teachers to be responsive in the moment look like? Can we design a routine which does not take an enormous amount of time for teachers to plan given the real time constraints faced by teachers? Can the instructional routine focus teachers and students more on understanding student reasoning rather than just identifying mistakes?
In their 2009 article entitled “Instructional Activities as a Tool for Teachers’ and Teacher Educators’ Learning,” Magdalene Lampert and Filippo Graziani introduced the idea of instructional activity for ambitious teaching. They define an instructional activity as “designs for interaction that organize classroom instruction”. Expanding on this definition to capture a distinction between instructional activities and instructional routines, instructional routines are “designs for interaction that organize classroom instruction”, shared amongst a group of teachers, that are repeated using different content and goals, frequently enough that both teachers and students can internalize the structure of the lesson.
These instructional routines could become a standard way of working that every other profession, aside from teaching, has developed to standardize and professionalize their work. I offer that these instructional routines are also the rich formative assessment-embedded activities that we have all been waiting for.
The greatest benefit of these instructional routines is their routine-ness. Instead of having to invent a different lesson plan or activity for every different mathematical idea, a teacher can select an instructional routine appropriate to the mathematics at task. Rather than having to re-invent teaching each day, planning teaching becomes more about choosing mathematical goals, selecting tasks to support those goals, and then embedding these tasks within an activity.
But why are these instructional routines useful for formative assessment? Let’s look at one instructional routine, Contemplate then Calculate, to see how it aligns with Dylan Wiliam’s definition of formative assessment introduced earlier. (Here are other examples of instructional routines)
Here are some key elements that teachers need to consider when implementing instructional routines in their classrooms and their relationship to formative assessment.
Lesson preparation
In enacting this kind of instructional routine, a teacher needs to select a mathematical problem, ideally one rich enough for students to have something to talk about and one that will focus students on a particular mathematical goal. Once a task is selected, in order to make the best use of the instructional time with their students, this teacher anticipates the different approaches her students might make.
For example the task selected might ask students to identify the number of white squares in the following image without counting all of them. In this case, the goal is to support students using mathematical structure (Common Core Math Practice 7) to identify ways of chunking the figure in order to make it easier to work with and to allow students to connect what they know about multiplication to counting squares. (Here are more sample tasks, each of which could be the mathematics that is inserted into the instructional routine).
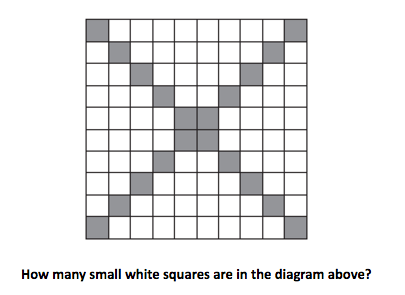
Before giving the task to students, it is useful to anticipate strategies students might use. For this task, one potential strategy is to chunk the diagram and notice that there are four identical triangle-like shapes. One can then zoom into one of these triangles to see that it is formed of four rows, each of which is two squares longer than the row above it, so since we start with two in the first row, the triangle-like shape has 2 + 4 + 6 + 8 = 20 total white squares for one triangle-like shape. Since there are four of these shapes, there are 20 × 4 = 80 total small white squares.
By identifying potential strategies in advance, the teacher is better equipped to circulate around the classroom during the portion of an instructional routine where students are working together and listen to student conversations and observe them work. During the portion of an instructional activity where students are presenting their ideas, anticipating strategies makes it easier for the teacher to focus students on a particular mathematical goal and make the mathematics evident in the solution explicit for everyone through careful annotation.
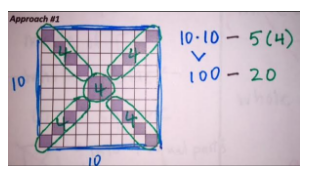
Here is an example of three annotations and three descriptions of student strategies. Which annotation goes with which strategy? How do you know?

Approach #1
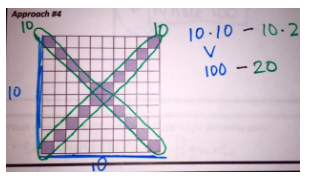
Approach #2
Approach #3
Description 1
“I chunked the shape into four triangle-like shapes and counted the number of squares in each row, and then multiplied this by four.”
Description 2
“I noticed five groups of four grey squares, which is 20 squares and I subtracted that from the big 10 by10 square to get the remaining white squares.”
Description 3
“I noticed that each row has 2 grey squares, so there are 20 grey squares because there are 10 rows. I then subtracted these from the big 10 by 10 square.”
By deciding in advance on various ways to annotate the task when students describe their strategies, teachers can shift their cognitive load while teaching from remembering what they want to say next to really listening to what students are saying and support other students in the class in doing the same.
The Parts of One Instructional Routine: Contemplate then Calculate
Lesson launch
This instructional routine starts with a launch designed to make it more likely that students understand both the purpose of the activity and their role within the activity. This script allows students to orient toward the goal themselves and aligns most directly with ‘clarifying the learning intentions’ formative assessment strategy. The meta-reflection activity at the end of the instructional activities helps students see progress towards those goals themselves as well.
Orientation to the task
Students are then given an independent opportunity to notice key features of a problem, followed by time with a partner to share what each noticed and briefly discuss how that could be mathematically useful. During this time, the their teacher circulates around the room and gathers information on what students are thinking about. Students are then gathered together for a whole classroom sharing of the mathematical structures, patterns, and/or quantities noticed. The teacher records these noticings so that they become the shared knowledge of all the students in the classroom. Because the cognitive demand of “notice” is relatively low, all students can participate in this orientation; because the noticings are shared, all students develop ownership of the task–long before any struggles would prevent their investment.
Partner work
Next, students use the gathered information to build and share a solution strategy while teachers have amply opportunity to circulate around the classroom and listen to what students think and use this as evidence of what they understand and more importantly, how they understand it. Since each instructional activity includes preparation work ahead of time where teachers anticipate the kind of thinking they expect, teachers are now better able to contrast their expectations of student thinking against the actual live student thinking they encounter.
By working within a structured routine, students also have less extraneous information to pay attention to in the mathematics classroom and are expending less of their total cognitive load on remembering what’s happening next and what their role is now; therefore, they are better equipped to pay attention to each other and to the mathematical ideas surfacing in the classroom. When students are able to pay closer attention to how each shared mathematical idea works, students get better feedback about their own ideas. Both of these observations are also true for teachers.
Sharing and studying strategies
Now the teacher orchestrates a whole class discussion around the mathematical focus for the day. The objective here is to use the thinking students have done and explicitly make this thinking public for everyone to understand by probing students for more detail, asking students to listen to and restate each other’s ideas . As a group, the role of students is to work as mathematicians do, by constructing and assessing arguments for the validity of their mathematical approaches and looking for connections between the various ways the class solved the problem for today.
During the partner work and sharing out portions of the activity, students are oriented not to the teacher’s talk but to each other’s speaking and thinking, which activates them as resources for each other. When the strategies conjectured by students are unpacked and made explicit for students through gesturing, annotation, and restatement, students can make clear sense of what mathematics is being discussed and why it works (or in some cases, why it does not work).
Meta-reflection
Since the goal of mathematics classes is not to learn how to solve individual problems, but to use problems to learn mathematical ideas, many of the instructional activities include a meta-reflection portion of the activity. Here students respond to a prompt or write about what they learned during the lesson. Ideally students should be able to describe what they learned in relation to the goal articulated at the beginning of the lesson.
Conclusion
“Instructional routines support teachers in studying the impact of teaching practice on student learning by focusing attention on the outcomes of a small, well defined, common set of practices that are repeated for a given period of time.” (Deeper Learning, Magdalene Lampert, 2015) The goal of these activities is to allow teachers to better study their own impact and to allow students to better see their progress in learning mathematics over time–to see themselves as doers of mathematics. Simultaneously, the same features that make instructional routines useful tools for developing teacher practice support teachers in integrating formative assessment practices as part of their teaching.
Formative assessment is not an exit ticket at the end of a lesson or a quiz every Friday. It is a framework for teaching and as such an instructional routine which aligns well to the framework is more likely to be useful for teaching than any attempt to layer formative assessment strategies on top of an existing set of routines.
Blue says:
Really like the closing paragraph here.
August 10, 2017 — 9:06 pm