Tag: The Reflective Educator (page 7 of 43)

My colleagues and I have formed a journal study group where we intend to share pieces of research which are interesting, and have some compelling story to tell about understanding research. I’ve chosen Benny’s Conception of Rules and Answers in IPI Mathematics by Stanley Erlwanger. In order to support our discussion of the research, I’ve created a few slides which I have shared below. I recommend opening up the speaker’s notes in order to understand the presentation better.

1. Life isn’t fair. Do something about it.
    
2. The world may not care about your self-esteem, but having a healthy self-image is more likely to lead to positive relationships with the people to whom you are close and having healthy relationships is the key to having a happy life.
    
3. Don’t focus on the money. Focus on improving yourself and doing good work. Both of these are more valuable than money.
    
4. Don’t work for a boss. Work for yourself. Be tough on yourself, but not so much that you crack. Life is hard work, and it’s short, and there’s no reason you should spend it following someone else’s orders. If you work for yourself, you don’t need to start at the bottom and work your way up.
    
5. You will make mistakes. Don’t look to blame someone, learn from them.
    
6. Always clean up after yourself. Fix your mistakes, own up to them, before you look to fix other people’s mistakes. Expect others to own up to what they’ve done wrong.
    
7. In life you’ll find that those in power define winning and success so they are doing it, and you are not. Don’t let other people define for you what it means to be successful.
    
8. Don’t waste time worrying about what other people think of you. Vanity can be the death of innovation because every moment spent worrying about what the world thinks is time spent not thinking for yourself.
    
9. Don’t watch television. It will fill your mind with stereotypes, none of which will help you find your own path in life.
    
10. "Be kind, for everyone you meet is fighting a hard battle." ~ Plato
     
11. Bonus: Be insatiably curious about the world.

I’ve recently been tinkering with the format of an online webinar in an effort to make what happens in a webinar more engaging and "minds-on" for teachers.

The problem, as I see it, for most webinars is that the presenter spends 99% of the time talking during the webinar, while the participants, if they are lucky, are in a chat window, occasionally discussing what the presenter is sharing. I feel fairly certain that almost everyone in a webinar will at some point switch the window to work on some other task, whether it is tweeting, reading their email, or something else not related to the presentation.

It is important to remember that a webinar is not worth having if no one learns anything from the experience, and no one even considers if their current practice needs to change. It is equally important to remember that a webinar is not worth having if the participants would have been better off reading a book on the topic instead. For the cost of some webinars, participants could potentially buy several books to read themselves at their leisure, rather than have someone they cannot see read it to them. A free webinar is not really free; it has the cost of the time participants spend watching it.

What I have discovered is making a webinar something people can participate in more easily is challenging for a variety of reasons.

1. Most webinar software is designed to be something a presenter uses to share information. The bulk of webinar mechanics seem to be to ensure that participants are able to hear a presenter read their slides clearly.
2. While many webinar packages allow for participants to share their screens, the software limits screen-sharing to one participant at a time. I have yet to see a single webinar software package that enables participants to form smaller groups and share what they are doing with each other.
3. Screen space in a webinar is almost entirely devoted to what the presenter is sharing, rather than the discussion space where participants could potentially talk about the presentation. Imagine the physical space of your classroom was apportioned in the same way. Wouldn’t that seem a little bit ridiculous?
4. Application sharing, if it is present in the webinar software, virtually always restricts access to the application being shared to the presenter. Even if I wanted to give a participant a chance to play with a particular piece of software in front of the whole group, it is not possible to do so.

Here are some things I have done to try and alleviate some of these issues.

1. I share links to Google Docs and Spreadsheets in my webinars, so that participants can leave the webinar software and collaborate with each other to build something useful.
2. In a recent presentation on Programming in Math Class, I set aside 20 minutes of the webinar time so that participants could actually use the software I was recommending, and see what they could build with it.
3. I plan for questions from teachers to drive at least a portion of the presentation, and I modify my presentation as much as I can in order to suit the needs of the participants. This addresses the question; why I am teaching this, to this particular group of learners, in this particular way? If you don’t at least respond to, and modify your presentation based on questions from participants, you might as well have sent them a link to a video instead. At least they could pause and rewind the video as needed.
4. There are some software packages out there that address some of these concerns, but all of them have some pretty serious limitations. Google Hangouts allow for live document editing and application sharing within the Hangout window, but are limited to 10 participants. Mikogo addresses some of these issues as well, but is limited to 25 participants.

Here is what I would like to be able to do with webinar software.

1. I need to be able to form participants into groups, which are either randomly chosen, self-selected, or grouped by the presenter. In each group, participants should have shared access to software as designated by the presenter, or as each participant feels the need to share.
2. I’d like to be able to switch the view of the presentation as necessary so that the slides can shrink when they are unimportant and the shared workspace or chat window could expand as necessary.
3. I really want to be allow participants to collaborate on objects in any software during a presentation which they can take away with them later, and therefore exist outside of the presentation space.
4. I want to be able to designate presentation pathways, based on decisions I make during the presentation. If a group wants to see an example in more detail, or has a particular set of needs, I’d like to be able to switch the direction of the presentation on the fly, and choose a different set of slides to use to frame our discussion as needed.
5. This is a minor point, but I’d like to be able to do polls and get responses from participants within the software itself, in a way which makes sharing the results with all of the participants visible and intuitive to understand.

Imagine you are in charge of designing webinar software for the future. What do you want it to include?

Tonight my wife asked me why 4 – (-3) = 7. Apparently my son had "explained" it to her earlier tonight, but she hadn’t really understood his explanation. So I gave it a shot.

First I tried the same explanation that seemed to work for my son when he asked me what 4 – (-3) would be earlier today.

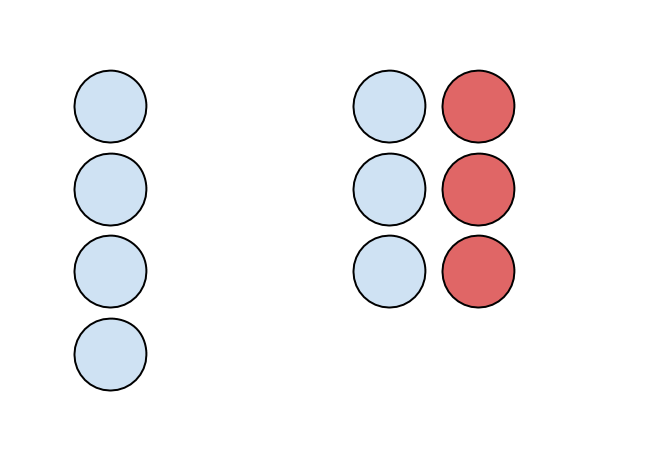
Me: "Imagine you had 4 blue circles, representing 4 positive 1s or 4 total. To this you add 1 positive circle and one negative circle. What would be the new total?"
My wife: "Still four. You added 0."
Me: "Okay, so let’s add 0 like this 3 times so the total will still be 4, right?"
My wife: "I get it. I don’t know why we are doing this, but okay."
Me: "So now, I take away the three negative circles, and therefore I am taking away a total of negative three from this picture and I’m left with 7. Therefore 4 – (-3) = 7."
My wife: "I don’t get it."

I tried a number line representation.

My wife: "I like looking at things on the number line."
Me: "Now imagine I’m on the number line at 4. If I subtracted 3, I’d end up at 1, so if I subtract -3, I must do the opposite, and so I end up at 7."
My wife: "I don’t get it."

Next, I tried operation consistency.

Me: "Okay, let’s try again. You agree that 4 + -3 = 1, right?"
My wife: "Yes. I understand that."
Me: "And 4 + 3 = 7 is obvious to you, as is 4 – 3 = 1. 4 – (-3) can’t be the same as 4 – 3, so it must be that 4 – (-3) = 7."
My wife: "That makes no sense."

I tried going back to the number line.

Me: "Okay, so what’s the distance between 5 and 2 on the number line?"
My wife: "3."
Me: "Right, since 5 – 2 is 3. Basically, one way to think of subtraction is that it gives you the distance between two points on the number line."
My wife: "Aaaaaah, I get it now."
Me: "So what’s the distance between 4 and -3 on the number line?"
My wife: "7. I get it, thank you so much. Who invented this rule anyway?"

(Aside: This is not quite true. -5 – -3 is a pretty good counter-example, but I’ll talk to my wife about that tomorrow.)

I decided to go back to mathematical consistency in a different way.

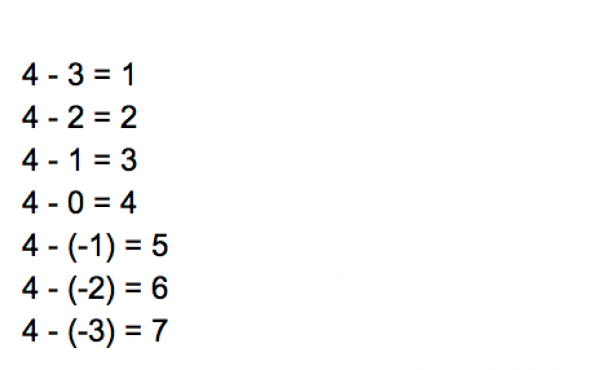
Me: "Okay, let’s look at the following pattern. 4 – 3 = 1, 4 – 2 = 2, 4 – 1 = 3, 4 – 0 = 4. What do you notice?"
My wife: "Well the thing you are subtracting is getting smaller, and the answer gets bigger."
Me: "What do you think would happen if I subtracted -1? What would make this pattern consistent?"
My wife: "Well 4 – (-1) would have to be 5 then."
Me: "Right. And so then 4 – (-2) = 6, and 4 – (-3) = 7."
My wife: "Okay. I’m going to ask our son to try and explain this to me tomorrow, pretending I don’t get it. I’ll let you know if his explanation makes more sense then."
 

Do you have any other models I can use, should this question come up again?

This is continued from here.

Imagine a scale for the open-endedness of a mathematical task.

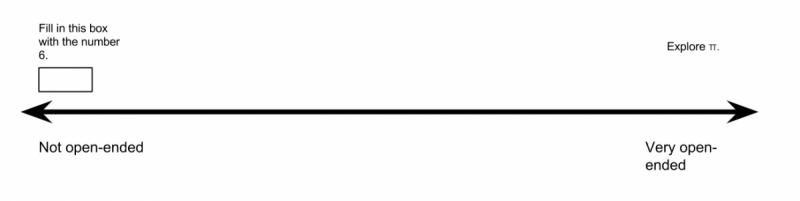
At one of the scale you learn a lot about what exactly kids can and cannot do but you sacrifice the opportunity for students to learn much from the activity. At the other end of the scale, you have no idea what children know, but you gain the potential for students to learn a tremendous amount. At one end of the scale, children know exactly what they are supposed to do, but at the other end of the scale, they may have no idea how to get started, and in doing so, learn very little as they struggle.

An ideal mathematics task for students is probably somewhere in the middle. A long term goal for any mathematics class should be to help students be able to cope with more ambigious mathematics activities than they were able to do before.

Try this mathematics problem, then continue reading.

Another issue that comes up with designing mathematics tasks is the hidden assumptions people make when you give them problems. When you read that problem, how did you imagine that loaf of bread in your head? How did you define the word cut? How many people are sharing the bread? The answers to these three questions will determine to a large extent what your solution to this problem looks like. This means that when designing mathematical tasks, we not only have to consider how we have written the task, we also need to consider how students may read the task, and what assumptions they are likely to make.

Context clues also matter. Notice how this version of the problem adds a pretty large context clue. What differences does this make in how students respond to the task?

Now look at this variation in the task.

Technically, this question is the same mathematical problem as the first two, but it will end up with a much wider variation in responses than either of the first two problems will. All we have changed is the context the student is presented with when they are given the problem.

This leads us to two methods for changing the open-endedness of a mathematical task.

1. Change the context of the problem to make the context more abstract.
2. Change the inherent assumptions in the problem, or at least point out that those assumptions exist.

In a future post, I will explore more ways to consider the open-endedness of a mathematical task, and offer some suggestions on ways to change standard mathematical tasks, while still giving students sufficient scaffolding to know where to begin.

Tomorrow, thousands of educators from various different countries are expected to attend a free 3 day virtual conference, The Reform Symposium, #RSCON4. RSCON will be held October 11th to 13th in conjunction with Connected Educator Month. The entire conference will be held online using the Blackboard Collaborate webinar platform. Participants can attend this online conference from the comfort of their homes or anywhere that has Internet access. This amazing conference provides educators new or currently active on social networks the opportunity to connect with educators and professionals in the field of education worldwide.

Useful links (click on any item for more information):

Opening plenary – Sugata Mitra, 2013 Ted prize winner and instigator of the Hole-in-the-Wall experiment, will speak about The Future of Learning.
Musical guest – Steve Bingham, the internationally renowned electric violinist, will conduct a live performance.
10+ international keynotes
4 panel discussions featuring distinguished experts
100+ presentations by educators around the world

I would like to thank the incredible organizers- Shelly Sanchez Terrell, Steve Hargadon, Clive Elsmore, Chiew Pang, Kelly Tenkely, Chris Rogers, Paula White, Bruno Andrade, Cecilia Lemos, Greta Sandler, Peggy George, Marcia Lima, Jo Hart, Phil Hart, Dinah Hunt, Marisa Constantinides, Nancy Blair, Mark Barnes and Sara Hunter.

I will be presenting for RSCON4 on Sunday night at 7pm EST on Programming in Math Class, using an active, participatory format. Slides from a similar presentation I did in San Francisco at IntegratEd are below.

As I was travelling to St. Ives, I met a man who’d lived seven lives,
In each life he’d learned seven lessons,
Within each lesson he’d had seven chances,
With each chance he’d made seven mistakes,
With each mistake he’d found seven connections,
How many connections, mistakes, chances, and lessons are missed by those who fear to live?

I grew up in a household that read all the time, talked about the world as we thought it exists and imagined possible worlds, and had conversations all the time about anything that interested us. I had my first computer at age 8, and had the freedom to use it as I pleased, which turns out involved programming it. My world was rich with numbers. My toys were mostly things that I could build things with. My house had a hallway full of many thousands of books, and so I never ran out of something to read.

When you say that I’m smart, I beg to differ; I come from privilege. Or if you insist on wanting to continue using the word smart, we should redefine it not to mean an inherent fixed trait that someone has and possibly inherited from their parents, and think of it as a trait that is developed by immersion in rich experiences. 

The objective of this workshop is to talk about different ways of making abstract ideas in mathematics more real for students. Sometimes this involves using various technologies, and other times it does not. I also want to create a set of slides for my workshop so that I can respond to the potential needs of the participants who come to the workshop. In general, the idea is pedagogy first, and then asking the question, what tools (technological or other wise) can we use to address the pedagogy?

Huge hat tip to Dan Meyer for making some resources that are particularly useful in addressing some of the pedagogical ideas I’m trying to explore with participants.

Any suggestions?

I may be presenting on social media use in education for a group of administrators in month or so, and a discussion I had on Twitter prompted me to think about why I use social media. An important aspect of any presentation on any tool is addressing the question; why should I use this?

Educators are right to be skeptical of social media use. It is commonly protrayed in the media as frivolous or inane. It can be time consuming. It is certainly the case that many people use social media as a distraction from the world around them. It is hard to convince educators that social media is worth the investment in time.

Given that there are obvious drawbacks to the use of social media, it is reasonable to ask, do the benefits outweigh these drawbacks?

I use social media to collaborate with people from around the world. I curated a presentation on different formative assessment strategies which has been viewed thousands of times. I did not create this presentation myself. I seeded it with 20 strategies for formative assessment, shared a public link tso that people could add to the presentation, and then made sure to keep the formating in place as people added their ideas to the presentation. Once the ideas stopped coming in, I closed off the document for editing, and refined the formating of the document.

I use social media to find out about things in education that are outside of my immediate world. I have heard people say that social media acts as a bit of an echo chamber, where ideas are bounced around and rarely challenged. This may be true to some extent, but if social media is an echo chamber, the typical faculty room is a linen closet by comparison. It is not that there aren’t great ideas that come out of discussions, there absolutely are, it is that the frequency of these ideas is a lot less, and they become stale more quickly.

I use social media to connect with people from around the world, share my project ideas with them, and get feedback on my work. I also get feedback from my colleagues at work on what I do, but educators are busy people. If I share something with my network, not only am I helping contribute to a growing pool of shared knowledge, a few people may help me find the bugs in my work, or even tell me that I’m completely crazy.

I use social media to discover that there are completely different ways of teaching. Teaching is a cultural activity, and to some extent we have a shared cultural knowledge of teaching, but it is also the case that there is a lot of variation within cultures, and between cultures. Cross-pollinating between different cultural understandings of teaching is a bit like preventing in-breeding by marrying someone from a different village.

I use social media to share my personal narrative with my colleagues around the world, and seek advice on how to change the ending.  I try not to forget that at the other end of each of the blogs I read, the tweets I see, and pictures that are shared, are people. These people have their hopes and dreams just the same that I do, and social media can act as a way for people to share their dreams, find other people who have the same dreams, and commiserate over our failures. While I do get lots of emotional support from my family and friends, I often have ideas that I want to discuss that are completely outside of their interest (actually, this is surprisingly common).

I use social media to transcend some of the social hierarchies of our educational society. Through social media, I discuss ideas with mathematics education researchers, professors of education, administrators, authors, and many, many teachers like me. Without social media, it is highly unlikely that any of these conversations would happen. In social media, it is more about your ideas (although not exclusively) than about who you are, what you look like, and where you work.

I use social media to learn when I have time, wherever I have Internet access, and whatever it is I feel like I need to learn. I am self-directed in my learning, and I am not restricted in what I learn to a small number of professional development days per year. Learning new things becomes something I do daily rather than monthly. Instead of having to spend my available time searching for or creating resources, resources come to me (although not always exactly when I need them).

Do these sound like compelling reasons to use social media? Can you offer suggestions for other reasons to use social media?