This year I have really tried to step up the process of bringing the real world into my mathematics class. A major focus has been on using technology appropriately as a tool to help solve real life problems.
Here are some examples:
Distance formula: Finding an optimal (or near optimal) solution to the Traveling Salesman problem for a small number of cities.
Basically here the students were given the assignment of choosing 6 or 7 cities fairly near each other on a Google map and finding the x and y coordinates of each city, then using the distance formula to determine the distances between the cities. Once they had this information, they were to try and figure out a shortest path, or at least something very close to the shortest path, and then justify their solution.
Linear graphs & Piecewise functions: Compare 4 or 5 difference cell phone plans.
Students should take a few cell phone plans and compare the plans, including the cost for text messages (which may include similar graphs), the cost for extras, start up costs, etc… I found the students end up needing to create piecewise functions in order to represent a cell phone plan which has a fixed rate until the minutes are used up at which point the customer has to pay extra for each minute.
Shape and Space: Design a new school building.
Here I showed the students the new lot our school is in the process of purchasing and our project is to design a building for that spot, and calculate how much their building design will cost (within the nearest $1000). It involves finding area, volumes, perimeters, scales, perspective, etc… We are using Google Sketchup for the designs but I am now trying to work out how to import the students designs into a virtual world (like OpenSim) so we can have each student group lead walk-arounds of their building.
Polynomials: Determine how many operations multiplying a 100 digit number times a 100 digit number takes.
Students are learning about computational complexity theory by analyzing the number of steps it takes to multiply numbers together. They record each step in the operation and increase the size of the numbers of each time and re-record their results. They then compare the different number of steps in each operation and try to come up with a formula, so that they can answer the 100 digit times 100 digit question. Our object: Figure out why our TI calculators can’t do this operation. It turns out that the formula itself is a polynomial, and their substitutions to check their various formulas count as a lot of practice substituting into polynomials, which was a perfect fit for our curriculum.
Quadratic functions: Create an lower powered air cannon and use it to fire potatoes a few meters.
Here the students are attempting to use quadratic math to try and analyze their cannon, then the objective is to try and hit a target with a single shot later. The cannons should be very low powered for obvious safety reasons, capable of firing a potato (or Tennis ball) a few metres at most. There is also a slight tie-in to Social Studies where my students will be studying cannons in their unit on medieval warfare.
Bearings and Angles: Set up an orienteering course in your field or local park.
Students attempt to navigate a course through a park and pick up clues at each station, which they use to figure out a problem. Students have to be able to recognize the scale on the graph, navigate using bearings, and measure angles accurately. Also lots of fun, we did this in Regents park for a couple of years in a row.
Integration: Calculate the area (or volume in a 3d integration class) of an actual 2d or 3d model.
Basically you have the students pick an object which they then find the functions (by placing the object electronically in a coordinate system) which represent the edge of the object, then place the object in a coordinate system and calculate area of the object using integration.
Percentages: Find out how much your perfect set of "gear" (clothing) costs when it is on sale and has tax added.
Students take a catalog and calculate how much it will cost for them to buy their perfect set of clothing. They can buy as many items as they want (with their imaginary money) but have to keep track of both the individual costs and the total cost of their clothing. You can also throw some curve balls at them, like if they buy more than a certain amount, they get discount, etc…
If you have any other examples of real life math being used in a project based learning context, please let me know. I’m always interested in other ideas, especially for the more challenging areas of mathematics. I’ll add more ideas here as I remember them.
 A typical classroom might look something like this. The problem with this arrangement that I see is that almost no one actually works under this arrangement. Why not? It’s distracting! this is similar to the layout in a lot of teacher staff rooms, and it is my experience that very little work happens in the staff room when it is full. There are too many people around and too many things to see and do.
A typical classroom might look something like this. The problem with this arrangement that I see is that almost no one actually works under this arrangement. Why not? It’s distracting! this is similar to the layout in a lot of teacher staff rooms, and it is my experience that very little work happens in the staff room when it is full. There are too many people around and too many things to see and do.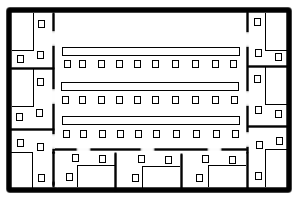 So I propose a different arrangement. Here’s a possible variation that might work. The big difference here is, students have their own workspace. They can work in their small groups with a few students working in the middle section, possibly under the guidance of the teacher. They have much fewer distractions available to them.
So I propose a different arrangement. Here’s a possible variation that might work. The big difference here is, students have their own workspace. They can work in their small groups with a few students working in the middle section, possibly under the guidance of the teacher. They have much fewer distractions available to them.