The Reflective Educator

Education ∪ Math ∪ Technology

Tag: computers (page 1 of 1)

June 7, 2013 / 0 Comments

Access to computers

President Obama recently unveiled a plan to have broadband Internet access in every school across the United States by 2018. There’s only one huge problem with that plan; according to the US government’s own research, as of 2006, there was only one computer for every four students, and many of those computers are old. Outfitting the rest of the students in the United States with a computer, and upgrading the existing ones to be useful, will come with a hefty price tag.

Include with the plan (linked above) is this statement: 

In addition to connecting America’s students, ConnectED harnesses the ingenuity of the American private sector get new technologies into students’ hands and support digital learning content.

I read this as, "We will use public money to buy computers for students via private companies" and very likely, those private companies will make enormous profits, given the size of the US education market.

Here’s a more creative solution: develop open-source hardware for schools, like the Raspberry Pi. Not only will the costs be lower in the long run (since the US government can then mass-produce the hardware for schools at cost), it will create jobs within the United States, and allow for innovation in the field through end-user adaptation.

There are a couple of arguments against this idea.

First, one thing that brings down the price of computers is production in mass scale. To this I say, the number of students in the US school system is more than sufficient to allow economy of scale to bring down prices to reasonable levels.

The second argument is that competition between different manufacturers of computers reduces prices, which to some extend is true. However, technology companies also artificially increase their profits in a variety of ways, including delaying new features for their computers to force turn-over of their devices when they introduce these features, and continuing to build their hardware for planned obselescence rather durability and life-span.

While I think that there are tremendous benefits to technology in schools, I also think that schools should use public money wisely. The United States certainly has the technical capability of developing high-quality, durable, open-source hardware. The question is, why aren’t they using it?

June 18, 2012 / 1 Comment

Kindergarteners programming

Here are two sample programs from a pair of kindergarten classes today (I took screen-shots of their program, and cropped them to fit in this blog).

 

Program 1:

Program 1

 

Program 2:

Program 2

 

I started the kindergarteners off the same way I started off third graders last week – they were to program me, and then program their partner. It worked fairly well, as most of the kindies could figure out how to get me to move in a square fairly easily, but an L turned out to be a stumper for a while, and a T was super hard. One could easily have done this entire activity with some adults (or older kids) willing to stand in as computers and be moved around by the kindies.

The idea of this activity is to get students thinking geometrically and systematically – if I want the computer to draw this shape, what do I need to do to get it to work. The key here is that the kindergarteners have to do the thinking, and what they showed me is that they are capable of some fairly advanced logical reasoning when pushed into it a bit. Most of the kindergarteners were able to get the computer to draw a square, or run way off the screen, and nearly all of their programs involved using the repeat function. I really found the students had to think to be able to do this activity, and to trouble-shoot when their programs didn’t work.

I would not advocate this activity replace moving around time, or other drawing time, but if you are stuck at the end of a year with nothing but worksheets to do, this could be an excellent replacement.

June 14, 2012 / 3 Comments

Programming with 3rd graders

Group 1

 

I did two things I’ve never done before – I taught 3rd graders, and I introduced elementary school kids to programming.

Yesterday, I started off by talking to the kids about how programs work on a computer, using the analogy that a programming language is like talking to a computer. If you can speak the language of the computer, you can make it do what you want it to do. I pointed out that all of them were much smarter than a computer since they can speak and understand English, and no computers can do this – at least they can’t carry on a conversation that passes the Turing test (yes, I mentioned the Turing test with a group of 3rd graders).

The first activity we did I called "Program your partner." It’s a pretty easy activity to set up. I told the students that computers only understand simple instructions, like step forward and turn left. So I partnered up the students, and I had one act as the programmer, and the other act as the computer. The programmer was to tell the computer what to do but they could only use the commands ‘step’ (which meant take one step forward) and ‘turn’ (which meant turn one quarter turn left).

The first challenge was to get their computer to trace out the path of an L on the floor with their movement. They switched roles for the next challenge, which was to trace out a T. The next challenge was to trace out a square, and then I introduced a new commend which I called repeat. I asked the students, "How could you use the repeat command to make tracing out a square easier?" They had a bunch of ways of describing the command, which all boiled down to exactly what one student said which was "Repeat 4 times – Step then Turn." The final challenge was to trace out 4 squares connected to each other, and for this activity I asked them to double check their program by tracing it out using pencil and paper. It was interesting to me that none of the groups seemed to have any difficulty abstracting from taking steps on the floor, to writing those steps on paper. In fact, every group came up with a slightly different way of writing down the output of their program (many of them included arrows so that they could keep track of the path actually traced).

We then gathered together in front a projector, where I showed the students how to start the Turtle Art software, and showed them the Forward and Right functions. At this point, I got stuck! I had used Turtle Art in Ubuntu, which has a slightly different interface, and I didn’t know how to actually run my program! So we experimented together and played around with the buttons on the screen, making sure to make copious use of the help button, and eventually we discovered the magic wand together. Getting stuck here was a valuable lesson for all of us, because while I explored how to debug my problem, the students got to see my thinking process live.

Next, we had the students self-organize into pairs and get a computer out, and try out Turtle Art for themselves. The first few programs the students created were pretty simplistic, but fairly quickly the students learned how to create more and more complicated shapes. One of their favourite things to do was to use the Forever loop, and see the screen flickering as a particular square or other shape they had created was repeatedly drawn. I didn’t really have anything specific for the students to do with the program at this stage, as I thought some free exploration would be more valuable.

Group 2

 

Some of the students created complicated loops, and others used the commands to draw. This particular student, as you can see from their screen, had 4 different commands, which she learned how to alternate to produce the diagram above. So she hadn’t learned how to create a procedure to draw the figure above in one go, instead she had internalized what each of the commands did, and then used them as one would use a paint brush.

At the end of the sessions, the students gave it an enthusiastic thumbs up. I discussed the success of the two days with their teacher, and she was pretty impressed with the students ability to come up with representations of their own, and to create somewhat complicated figures within a few minutes of using Turtle Art. We are considering doing a longer unit next year related to the use of Turtle Art.

The popularity of the event was summed up by one student who told me "I give this activity an infinity out of ten!"

 

February 1, 2011 / 4 Comments

Mumbo Jumbo

Algebra is just mumbo jumbo to most people. Seriously.

If you asked 100 high school graduates to explain how algebra works, and why it works, I’d guess that 99% of them couldn’t, not in sufficient detail to show that they really deeply understand it. Remember that I am talking about high school graduates, so these people have almost certainly had many years of algebra and algebraic concepts taught to them. Most of these people will only be able to give you some of the rules of algebra at best, and some of them don’t even remember that much.

Algebra is an amazing tool for solving problems though! Formulate a problem as an equation, and unless the equation is too complex, there is an algebraic algorithm to solve that equation, and hence the problem you formulated.

Maybe it is such a useful tool that people don’t really need to understand how it works, maybe they can get by without a deep understanding, but still be able to follow the rules of algebra and use it to solve problems. I don’t really buy that argument though, simply because people who don’t understand something are prone to make mistakes, and not be able to check their work with a reasonable level of accuracy.

Computers are also mumbo jumbo to most people. If you asked people to explain how computers work, most of them cannot. There are actually very few people in the world who can explain from start to finish how a computer works, and there is no one that can explain every single piece of a computer. Computers are still amazing tools though, and give people the ability to solve problems that would otherwise be intractable.

I think computers are a useful tool despite our lack of understanding of how they work. Like algebra, computers are a block box in which we put our inputs and get outputs and don’t understand how the inputs are related to the outputs. Given this similarity, we should look at other reasons why using a computer might be superior to algebra.

There are some significant differences between using computers to do computation, and using algebra to do computation. The first is that using a computer, the error rate is much lower. Obviously you can still press the wrong buttons, enter the wrong information, read the information the computer gives back to you improperly, so there is error, but I’d argue that this error is much less than the standard error rate for algebra. The second benefit of using computers is that they are much faster than doing even moderately complicated algebra by hand, including entering the computation into the computer. In the case that doing it by hand is faster, then I’d say you should do the calculation by hand. 

The largest difference between using a computer to do the calculation and using algebra is that algebra is a single use tool. It can only be used to turn an equation into a solution. A computer can be used for so much more.

Granted we should consider computational mathematics to be a broader tool than just plain algebra, if we want a more fair comparison with a computer, but I’d argue that all of the same problems exist with other areas of computational mathematics. As we increase the scope of computations we can learn how to use, the power of the computer becomes even more evident. It takes much less effort to learn how to compute a broader scope of problems using a computer than learning all of the individual computational methods. Witness the power of Wolfram Alpha, for example. Enter in a search phrase and all sorts of useful information comes up.

So in the consideration of using computers for solving computations, over a by hand approach, we can see postulate that the computer will produce less errors, be generally faster, and is more multipurpose than the pencil and paper model is. Furthermore, the computers can do a lot more as a tool than what you can do with algebra.

Another issue I see is that our current mathematics curriculums leave very little time to learn more important skills than computation. As Dan Meyer (@ddmeyer) points out, the formulation of a problem is more important than the actual solution. Learn how to formulate problems and understand how to verify that what you are doing makes sense, then spotting errors in computation becomes that much easier. Furthermore, I’d like to see mathematics education be much more grounded in what is relevant, than be a collection of different types of math which are taught for historical purposes or because they are the ground-work for calculus.

The question for me is, why aren’t we using computers more to do mathematics in elementary and secondary education? It can’t just be because people are scared of change, can it?

January 18, 2011 / 7 Comments

Computers should transform mathematics education

Stephen Shankland posted an interesting article on CNET today. Here is an exerpt from his article, which you should read in full. He says:

Clearly, children need some understanding on their own of math, and reliance on a computer has a lot of drawbacks. But computers can also aid those who otherwise would fall by the mathematical wayside, or let people with more advanced abilities bypass drudgery and move on to the challenging material. Graphing calculators can let many students explore curves and functions that realistically they’d more likely ignore if they had to plot them by hand.

My response to some of the negative comments about his article is:

Some of you have decided that using technology to handle calculations in mathematics is going to weaken student’s understanding of mathematics. I have to tell you, our student’s understanding of mathematics, and even the vast majority of people’s understanding of what mathematics is pretty bad. Awful. Horrible. I mean, really, really bad.

Mathematics is not about calculations. Mathematics is about understanding how our world works through the lens of logical reasoning and pattern forming, and then communicating our understanding of that process to other people.

Calculations are a tool in mathematics to understand a process. In my opinion, I want students to understand the processes and ideas that mathematics represents, not the calculations which short-cut that understanding.

Here’s an example that Gary Stager suggested to highlight this problem. Ask a typical math teacher to explain to you why "you invert the 2nd fraction and multiply instead" when dividing two fractions works. Ask them to explain the concept behind "inverting and multiplying" two fractions, and you know what, they can’t. They’ve learned a recipe for doing a calculation but have no conceptual understanding of why that rule works, and these are people who are teaching our children about mathematics!

We need to move away from the mindset that the most important part of the mathematics curriculum we teach is the rote calculations which can generally be done much faster on a computer, and towards the mindset that students need to be able to formulate problems, decide on appropriate mathematics to use to solve these problems, and then do the calculations on an appropriate device, and finally check that these solutions make sense. These are the steps that Conrad Wolfram and Dan Meyer (in their TED talks) outline as crucial to mathematical understanding, and I completely agree.

Mathematics education needs to change. Those people who want a "back to basics" approach and get rid of the calculators seem to think that this will improve the mathematics education in our schools. This is flatly not true.

If you ask a random sample of people, they either "weren’t very good at mathematics" and generally hated it, or a very small minority loved it. This opinion spans all age groups and goes back many years, far before the introduction of calculators in schools. If we judge the success of an educational approach by the number of people who enjoy working in a subject, why are so many people who were exposed to that approach before the introduction of calculators hate mathematics so much?

Maybe we need to rethink our approach?

November 20, 2008 / 2 Comments

Working with a 1 to 1 laptop program

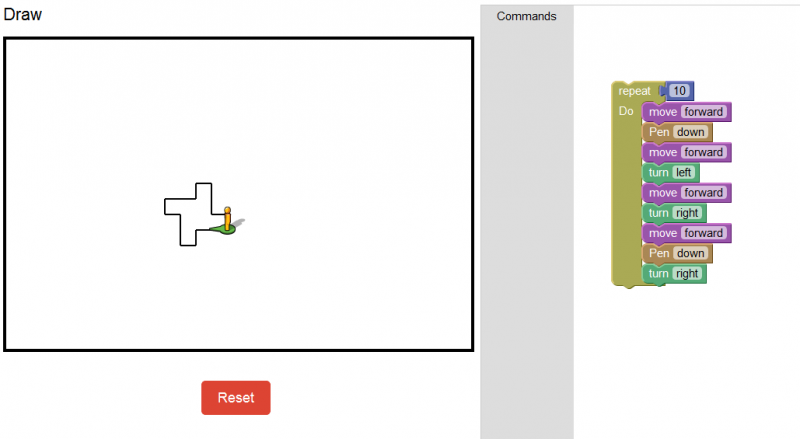
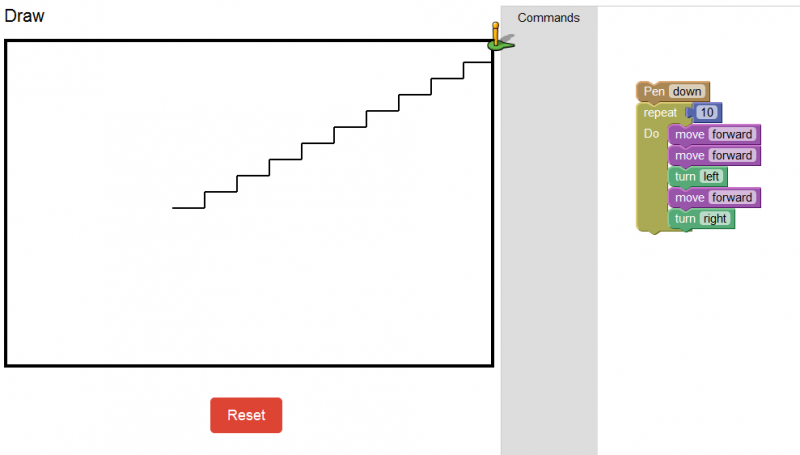
At our rather large high school in Thailand, we have a 1 to 1 laptop program.  Every student in the high school has a laptop, which they are supposed to bring to class.  After a year and half working with these laptops, I discovered the joys and pitfalls of such a system.

The really nice thing about the laptops is that you can plan activities that require a computer much more easily than schools where you have to book time in a computer lab.  Having done both, the laptops are just plain easier to work with.

Another advantage of the laptop program is that a greater percentage of the students you work with have an intermediate level understanding of how their computers work.  They can manage their documents in a relatively organized fashion, install software, navigate the web, and use a search engine, all with relative ease. It has been very rare when I have not been able to explain to one of my students how to accomplish a task.  I find myself being able give instructions to the students using higher level skills and more complicated phrases than my previous school.

For example, I can tell the kids to ‘copy and paste’ and to ‘create a screen-shot’ and most of the kids know how to do this stuff.  I can also give instructions like ‘copy the URL for the image and paste it into the textfield on the image uploader’ and they can do it.

Another nice feature of the 1 to 1 laptop program is that it allows me to include a little bit of tech training in my lessons.  Since it is likely that the students will be using a computer pretty regularly for the rest of their lives, it seems to me that the use of a computer is one of the most important skills I can pass along to my students.

Since the students have access to a computer at any time, you can use a number of online tools quite effectively.  I have mentioned in a previous article about using Google Docs for collaboration online, and with my classes I have also successfully used blogs, wikis and other resources I have found online with my students.

There are a number of problems with the use of the laptops however which need to be pointed out.

The first problem is that if you plan a lesson that involves everyone needing a laptop and one or more students does not have their laptop, you can find yourself going to your backup pretty quickly.  Students have difficulty keeping their laptops virus clear because of all of the file sharing they do.  They also sometimes just forget their laptops at <insert the location here>.

Another problem, at least at our school, is that there seem to be some limits as to how many students can access a wireless acccess point at the same time.  So once the first 15 or so students in your class get started, the next 5 or 10 students are locked out.  This can be pretty frustrating pretty quickly.

Students will also tend to use their laptops for inappropriate things during your lessons.  The student in the back that you think is diligently using their laptops for taking notes is probably text chatting with their friend in Physics or Biology.  Students who are supposed to be carefully working from a PDF version of their textbook are actually surfing blogging sites looking for next year’s fashion.  This can be real problem, and as usual you need to rely on your own classroom management skills to try and curb this kind of behaviour.  Some schools install special software on the network server to limit students access to the internet, but the kids in your class will probably just turn to computer games instead.

When all is said and done, I have enjoyed the access to a 1 to 1 laptop program I have had at my current school.  There have been some problems, but they have not been insurmountable.  It is likely that more and more schools will be looking to initiate similar programs, so we as educators must prepare for the future.

Archived posts

Calendar

November 2024
M T W T F S S
 123
45678910
11121314151617
18192021222324
252627282930  

Subscribe