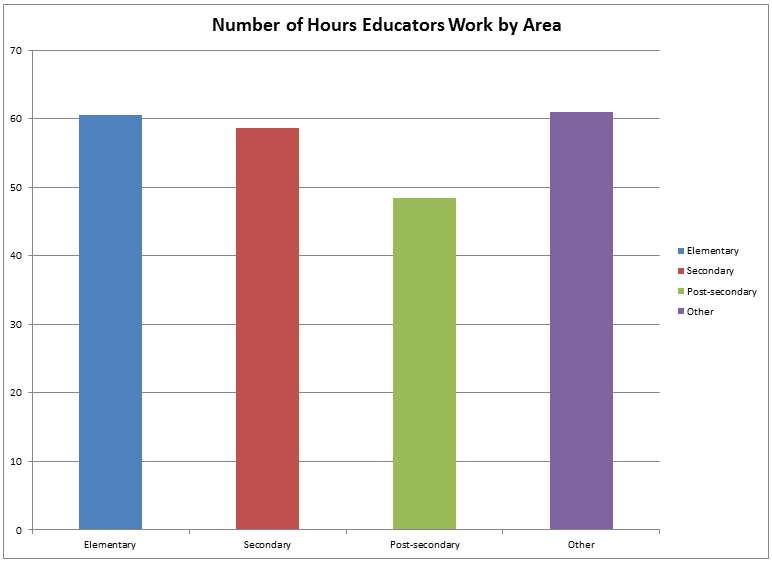
Research, by itself, rarely changes teacher practices. Presentations on why their practices should change rarely change teacher practices. Attending conferences rarely changes teacher practices (a teacher may adopt a few new things from a conference, but how often has a teacher come back from a conference and begun to teach in a completely new way?).
What does change teacher practice?
Eric Mazur, in his lecture "Confessions of a Converted Lecturer", recounts how standard measures told him his teaching style was sufficient, but when he applied a different measure, he was quite surprised to discover that his teaching had nearly no effect on his students’ conceptual learning of physics. The evidence that convinced Eric that his teaching needed improvement was the results of investigating his own teaching using a different tool, the force concept inventory. The key here is investigating his own teaching, not necessarily the tool he used.
In an essay titled, "How One Tutoring Experience Changed My Teaching", Sara Whitestone recounts how she discovered that the writer’s voice in their writing matters, and how she had to do more to help her students develop their own voices, rather than adopting the writing voice of their teacher. The tutoring experience is not what changed her teaching, it was her reflection on that tutoring experience that changed it, but the experience acted as a catalyst for this reflection.
When I asked the question, what evidence shifts teacher practices, on Twitter, I had a few responses, which could be summed up with these two tweets.
Why do teachers often ignore evidence? It is probably because the evidence they are presented is not grounded in their own experiences, but in narratives of experiences other people are describing. In other words, the way they are presented with the evidence is not supported by their experiences, and so they do not learn from it.
It seems therefore, that if we want teachers to change practices, one method which may work is to ask them investigate for themselves what their practices are, and participate in an inquiry into their own teaching practices.
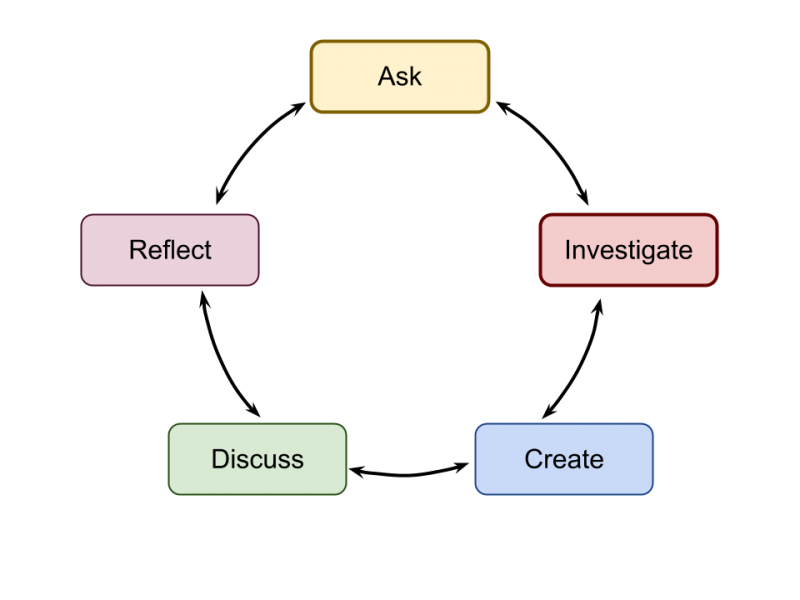
(Adapted from this)
What are some ways that you know are effective in promoting teacher growth and change of practices?