Year: 2014 (page 2 of 5)

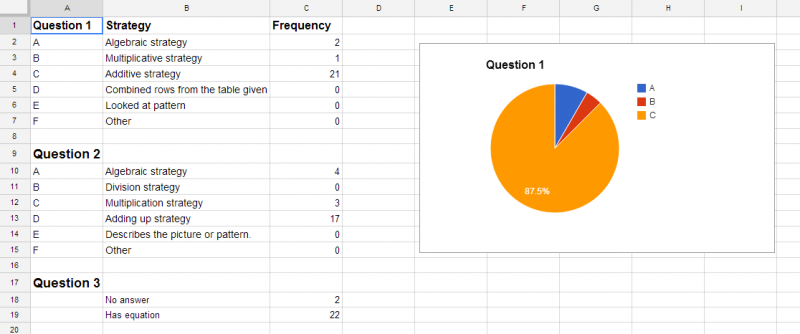
Here’s an approach to teaching about the relationships between the different forms of the equation of a line that is based on constructivism.

1. Be clear with students what the objective for the lesson is today.
2. Give students a tool for looking at the relationships between the different forms of the equation of a line.
3. Ask them to write down what they notice and what they wonder after they have played around with the tool themselves. Circulate around the room to see what they write down so you can better make use of it in the whole group discussion.
4. Next, as a group, discuss what students notice and what students wonder about the graph, or use a different talk protocol.
5. As a group summarize what appear to be the most important observations made, and everyone (including the teacher) writes them down. If important points about these representations of a line are not brought up, either ask questions to prompt students to realize these points themselves or make a note to yourself to structure a task that will help draw out these points next time.
6. Come back to this concept multiple times in a variety of different ways over the next few weeks, and even find ways to connect to this topic through-out the rest of the year.

Here’s an approach to this same lesson based on cognitive load theory.

1. Be clear with students what the objective of the lesson is for today.
2. Give them notes on the different forms of the equation of a line and some worked examples.
3. Give students twenty or so practice problems to do themselves. Circulate around the room while students do this and give them timely, efficient, and useful feedback.
4. Quiz students on their understanding of the concept. Use this to guide your planning in subsequent lessons.
5. Review this concept with students at spaced intervals over the course of the rest of the year.

My recommendation is that if you are unclear on how either of these approaches is helpful for students, then you should try it at least once. I have in fact tried both of these approaches myself, and I’m quite clear on which approach helps students make better connections to other areas of mathematics, and which approach did not work.

Which approach is more likely to lead to an instrumental understanding of mathematics? Which approach is more likely to lead to a relational understanding of mathematics? For reference, here’s a comparison of instrumental to relational understanding.

This is a video of Magdalene Lampert taking about Ambitious Math Teaching. I’m sharing it mostly so I don’t forget where it is.

I read an important passage in Elizabeth Green’s book “How to Build a Better Teacher” and decided that I had missed something important when reading about Magdalene Lampert’s teaching. Below is a summary of some of the important features of her teaching as I see them. The first tweet is the thing that I had misinterpreted as students talking to justify their reasoning, which is similar but not exactly the same as students talking to prove their reasoning is correct.

I’m tired of having to search all over the place to find the-link-to-that-mathematics-resource-I-really-want-now-and-bookmarked-a-year-ago and so I created a spreadsheet to keep track of the various mathematics resources as I learn about them. Yes, I know I could have done this with Diigo or Delicious, but I prefer the portability and simplicity of a spreadsheet.

I’ve opened the spreadsheet up for editing and will curate it to ensure it only includes what I consider to be the highest quality resources. The spreadsheet contains the categories of websites, mobile apps, software, books, research, and organizations. If you have a suggestion for a resource you think I should include, please offer it below, or add it to the spreadsheet. Note that I have currently protected the first sheet (the list of websites) so that you can comment on it, but not edit it directly.

This is by no means complete and will continue to evolve over time as I learn about new resources.

NCTM recently asked for Grand Challenges that are ambitious but feasible, positively impacting many people, and which should capture the public interest. Here is my grand challenge:

• Develop a comprehensive, national professional development model that supports the high quality mathematics instruction they have been promoting for many years.

Here’s what I think that could look like:

• We start by norming between a fairly large team of mathematics educators a core set of high quality mathematics teaching practices are, and what they look like in a real classroom.
• We then carefully study (to ensure that the practices work) and implement these practices in model classrooms where the educators who have previously normed continue to study their practice while continuing to discuss and collaborate with the original group of educators.
• These classrooms should be substantially open to the public (perhaps through video cameras, one-way glass, etc…) so that other educators, parents, and policy makers could come and visit the classrooms.
• Once each original educator has established clear evidence (from evidence of student learning) that they are able to consistently and reliably use the set of core practices (along with whatever other practices they have developed), they start norming their practices with another group of educators.
• This process continues until we have created a substantially similar core set of instructional practices that fairly large group of mathematics teachers consistently use.
• Two of the core practices we would establish are the teacher as researcher into their own practices and the collaboration with other educators to study each others practices to see what works.

There are some other core practices that I think that every mathematics teacher should do, but the most important core practices are to study your own practice and to collaborate with others in doing the same. Once this is established, then at least when each of us is experimenting with a different practice it will be easier for us to see the connection between what we do and student learning.

Here are some other ideas I think are also worth pursuing.

• Develop teacher training models at scale where teachers spend at least six months in close apprenticeship with an experienced classroom teacher with time to reflect on their emerging practice during this time. Follow this up with at least two years of additional support.
• Support many (one in every major city) smaller TMC-like mini-conferences with the overall aim of building local communities of mathematics teachers. Continue support of these groups by creating online space for these educators to continue their conversations and share resources with each other.
• Actively support the use of online professional development to increase the number of mathematics educators connecting with each other.

Imagine you are asked to learn about something, and the only way someone can help you understand it is with words, because there are too few examples of it around to actually see it for yourself. You think you know what it is they are talking about, but you keep getting confused because your image of what it is seems so much different than what the other person is describing.

It gets worse because most of the other people you talk to haven’t really seen it before either, and are relying on a story they read about it once before in a book or occasionally on their attempts to tell the story to other people. They sometimes contradict each other, and then other people come in and start telling a totally different story. In fact you aren’t listening to just one story, but many different stories all at once.

When you were growing up the story you were told was pretty different. None of your friends or family knows this new story. In fact, you were never told this story in school or even university. You don’t even really understand why you are being asked to listen to this story because as far as you are concerned, the story you had growing up was a perfectly nice story. Why come up with a new story?

You try and tell the story yourself, but it turns out the story is so different from any stories you have ever heard that it is hard to remember all of it at the same time. You make a lot of mistakes telling the story and feel discouraged and decide you should just stick with your old story. It’s a lot easier to do, and virtually everyone you know seems to value it a lot. Gradually you stop trying to tell the story, and stick with the older story that you undersntand very well.

This description pretty much exactly summarizes a reason why I think math education is so hard to change. The narrative around the changes necessary is often just too different than people’s personal experiences of learning mathematics.

For the last two years, the project I am currently working with has been asking teachers in many different schools to use common initial and final assessment tasks. The tasks themselves have been drawn from the library of MARS tasks available through the Math Shell project, as well as other very similar tasks curated by the Silicon Valley Math Initiative.

Here is a sample question from a MARS task with an actual student response. The shaded in circles below represent the scoring decisions made by the teacher who scored this task.

This summer I have been tasked with rethinking how we use our common beginning of unit formative assessments in our project. The purposes of our common assessments are to:

• provide teachers with information so they use it to help plan,
• provide students with rich mathematics tasks to introduce them to the mathematics for that unit,
• provide our program staff with information on the aggregate needs of students in the project.

We recently had the senior advisors to our project give us some feedback, and much of the feedback around our assessment model fell right in line with feedback we got from teachers through-out the year; the information the teachers were getting wasn’t very useful, and the tasks were often too hard for students, particularly at the beginning of the unit.

The first thing we are considering is providing more options for initial tasks for teachers to use, rather than specifying a particular assessment task for each unit (although for the early units, this may be less necessary). This, along with some guidance as to the emphases for each task and unit, may help teachers choose tasks which provide more access to more of their students.

The next thing we are exploring is using a completely different scoring system. In the past, teachers went through the assessment for each student, and according to a rubric, assigned a point value (usually 0, 1, or 2) to each scoring decision, and then totaled these for each student to produce a score on the assessment. The main problem with this scoring system is that it tends to focus teachers on what students got right or wrong, and not what they did to attempt to solve the problem. Both focii have some use when deciding what to do next with students, but the first operates from a deficit model (what did they do wrong) and the second operates from a building-on-strengths (what do they know how to do) model.

I took a look at a sample of 30 students’ work on this task, and decided that I could roughly group each students’ solution for each question under the categories of “algebraic”, “division”, “multiplication”, “addition”, and “other” strategy. I then took two sample classrooms of students and analyzed each students’ work on each question, categorizing according to the above set of strategies. It was pretty clear to me that in one classroom the students were attempting to use addition more often than in the other, and were struggling to successfully use arithmetic to solve the problems, whereas in the other class, most students had very few issues with arithmetic. I then recorded this information in a spreadsheet, along with the student answers, and generated some summaries of the distribution of strategies attempted as shown below.

One assumption I made when even thinking about categorizing student strategies instead of scoring them for accuracy is that students will likely use the strategy to solve a problem which seems most appropriate to them, and that by extension, if they do not use a more efficient or more accurate strategy, it is because they don’t really understand why it works. In both of these classrooms, students tended to use addition to solve the first problem, but in one classroom virtually no students ever used anything beyond addition to solve any of the problems, and in the other classroom, students used more sophisticated multiplication strategies, and a few students even used algebraic approaches.

I tested this approach with two of my colleagues, who are also mathematics instructional specialists, and after categorizing the student responses, they both were able to come up with ideas on how they might approach the upcoming unit based on the student responses, and did not find the amount of time to categorize the responses to be much different than it would have been if they were scoring the responses.

I’d love some feedback on this process before we try and implement it in the 32 schools in our project next year. Has anyone focused on categorizing or summarizing student types of student responses on an assessment task in this way before? Does this process seem like it would be useful for you as a teacher? Do you have any questions about this approach?

I’ve been working hard to read research carefully, both research with which I agree, and research with which I disagree. I still struggle with my tendency to overlook the flaws in research with which I agree, and to find fatal flaws in research with which I disagree.

This does not mean that I should ignore research; only that I continue to be careful to read all research with a critical eye, and discuss the findings with other people. My suspicion is that norming about what research means with people who have a wide variety of view-points might reduce my tendency toward personal bias.

Here is a one minute summary of a post I wrote about why we teach math.

I created this summary video as part of an application for TED@NYC. I think my odds of being accepted are improbably slim, but the opportunity cost is low.

What constitutes “good teaching” is not a well defined term. My evidence for this claim is that so many organizations appear to use very different exemplars of good teaching when sharing their work.

For example, this is considered good teaching by the Whole Brain Teaching institute.

The Program for Complex Instruction would likely define this as good teaching.

Seymour Papert, and other constructivists would likely define this as good teaching.

People who follow John Sweller‘s (and company) work on Cognitive Load Theory might offer this as an example of good teaching.

People who believe that the future of education lies in personalized education might offer this example as good teaching.

All of these methods of teaching are very different from each other. Would people who use these methods agree on what good teaching looks like? There would likely be some overlap, but if you took a representative of each of these teaching methods and asked them to observe a classroom (which as far as I know has never been done), I would be willing to bet that it would be very unlikely that they would agree as to whether or not the teaching they observed was “good teaching”.

A better measure of effectiveness is to look at the goals of the teaching, and the impact the teaching has on the learners in terms of meeting these goals. If you have x goal for your students, how much impact does your teaching have on your students? “Good teaching” would be therefore defined as teaching that has a greater impact on achieving a specific goal, and consequently, we are not able to define “good teaching” without knowing the goals. In the examples above, it is hopefully clear the goals of each the users of each teaching method are different, and consequently each of these could be considered good teaching, within the set of goals defined.

What goals do you have for your students? Are your goals the right goals for your students? Who has defined the goals for your students? How do you know if your students are closer to achieving your goals than when you started teaching them?

If you can answer these questions, you will be a lot closer to knowing what kind of teaching you should be using, and whether or not it is effective.