Year: 2011 (page 21 of 28)

April 14, 2011 / 1 Comment

Most livable city

We had Daanish Ali, the producer of the video below, come to our school and share his film with us (embedded below). I strongly recommend that if you live in an urban centre, you should watch this video. While it talks about water issues in the downtown East Side of Vancouver, I’m sure that similar issues exist in every major city in the world.

It is a great starting place for a discussion about urban water use, and very accessible for your students. Our kids finished watching the video and had some great questions.

Most Livable City from Pull Focus Films on Vimeo.

April 14, 2011 / 2 Comments

Free tools for math education

Here are some tools which I’ve either used (or explored) for mathematics education. They aren’t all open source, but they are all extremely useful, and they are all free to use (free as in free beer, some of them are also free as in free speech).

Geogebra

Geogebra image

This program lets you explore algebra and geometry, much like it’s proprietary cousin, Geometer’s Sketchpad. Having used both, I actually prefer Geogebra because I find it to be more flexible and easier to use. It will run on many different platforms including Windows, Mac, Linux, Android, and iOS.

Mathematics Visualization Toolkit

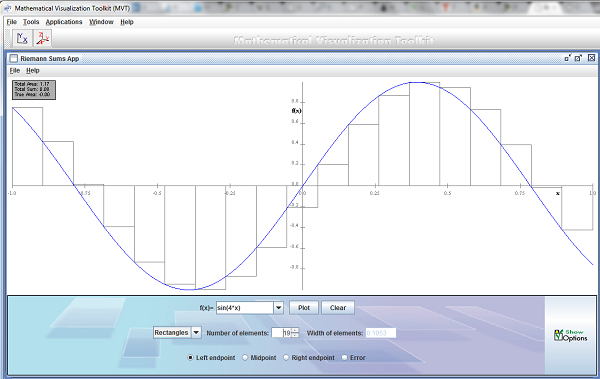
MVT screenshot

The Mathematics Visualization Toolkit is exactly that, a program which lets you visualize mathematics. You can use it to build complex visualizations, or you can use the visualizations which are already included (which are awesome by themselves). You can either use the web start version of the toolkit, or download an offline installer.

Scratch

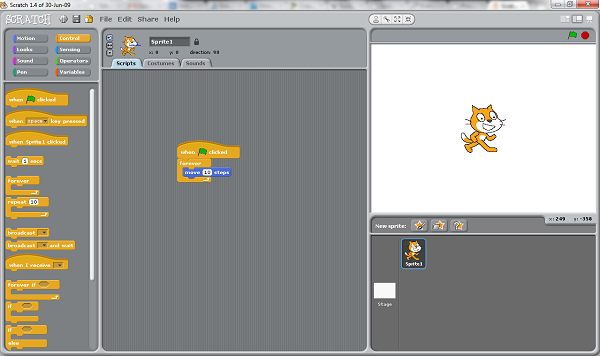
Scratch screen-shot

Scratch is an excellent program for learning programming but also mathematics like variables, sequences, Cartesian coordinates, and other useful mathematical concepts. Developed at MIT, it is a free download and includes a strong user community to seek help, and see what else can be done with the program.

Netlogo

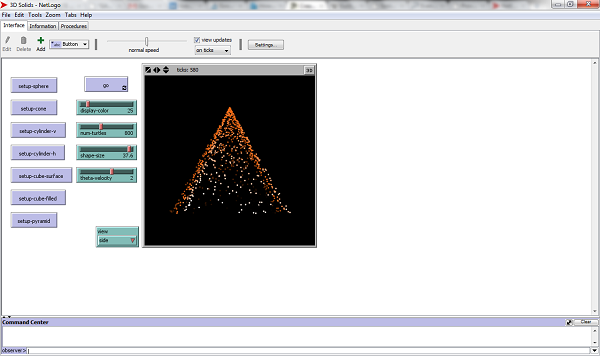
Netlogo screen-shot

Netlogo is “a multi-agent programming modelling environment” (According to the Netlogo website). It comes with hundreds of models for all areas of science and mathematics preprogrammed. It is a free download and will work on any computer which has Java 5 or later installed.

Audacity

Audacity is an open source audio editor and recorder. One example use in mathematics is to record a bouncing ball, and use the visual data from audacities recording to turn this into a graph of bounce versus time between bounces. You can also use it so students can record 60 second podcasts explaining some aspect of mathematics.

Calculize

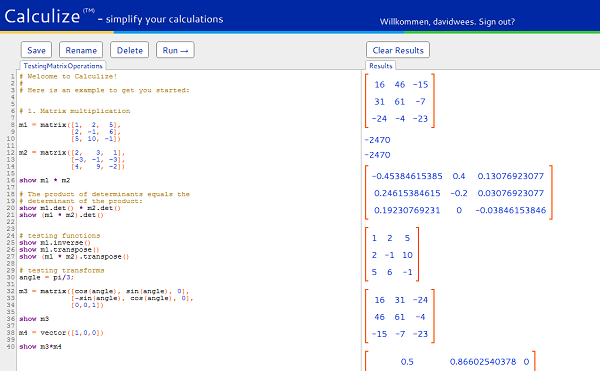
Calculize is a free (currently) web app which lets students perform mathematical computations using a reasonably simple programming language.

Wolfram Alpha

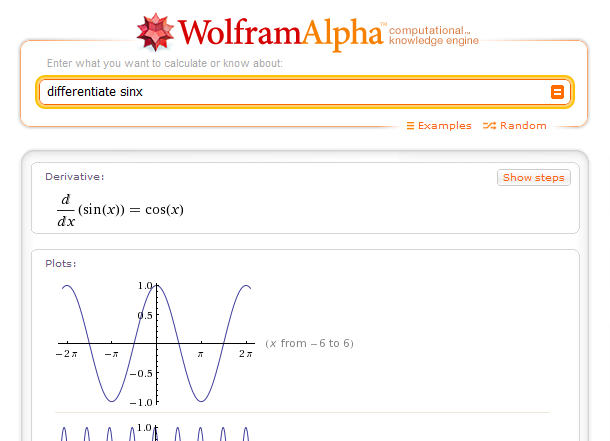
Wolfram Alpha is a computational engine built on top of the Mathematica architecture. It is amazingly powerful, and turns some homework assignments into a breeze. Recommendation: change your homework assignments, or do away with them all together.

Desmos

Desmos screenshot

This is a free online graphing calculator. It emulates a lot of the functionality of a typical graphing calculator but with a much easier to follow user interface and without much of the non-graphing functionality of a graphing calculator. It is easy to create graphs, and then share those graphs with other people. It is also currently in development, so it is still improving over time with new features being added every couple of months.

Logo

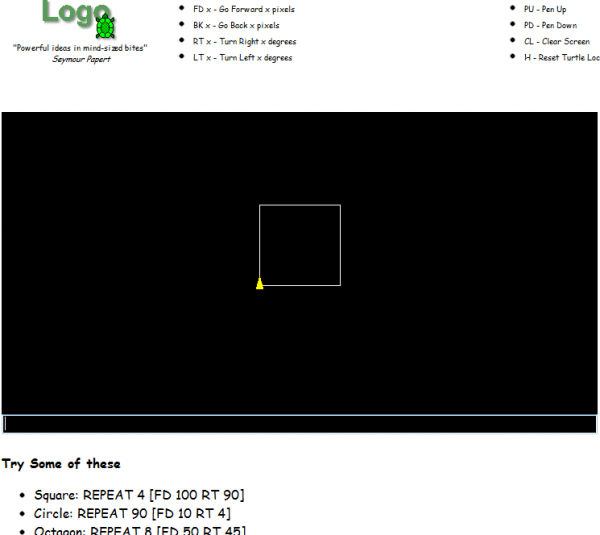
This Logo emulator lets students play with the classic programming environment Logo, built for kids by Seymour Papert and his colleagues at MIT, all online. It requires Java, but should run on most computers (sorry, no iPads…).

Google Earth

Google Earth is free (but proprietary) software that allows students to explore the world in 3d. One could use it for GIS applications, or even to explore the relationship between our 2d mapping system (longitude/latitude) and 3d space.

Google Sketchup

Google Sketchup (another free, but proprietary program) that allows students to create highly complex (or very simple, if they prefer) models. I’ve used it to have students construct their “ideal” school, and then from this model, they calculate the cost to build their school.

Screenr

Screenr is a free (for up to 5 minute recordings) screen-casting (think record your screen as a video) software. Some possible uses of it are for students to use it to create video tutorials, record their process of solving a problem, or create their own video word problems. Another alternative for screen-casting is Jing, but it publishes to a format which is harder to share in the free version.

Endlos

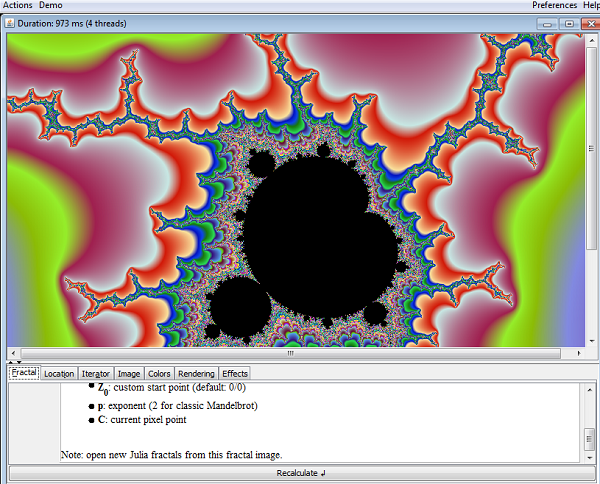
Endlos is an open source fractal generator which I’ve found runs very fast. It runs in Java, so it should run on any computer capable of supporting Java. The ability to experiment with, and explore fractals is a very interesting thing for students to do, but very tedious to do by hand…

The Number Race

The Number Race is an open source program intended to help students who have dyscalculia develop their number sense. It has many levels of difficulty, and runs in Java, which means it should run on a wide variety of computers.

Code Cogs equation editor

Code Cogs online equation editor

This free to use online equation editor could be a nice way for students (and teachers potentially) to construct equation images for use in a website.

Eigenmath

EigenMath

Eigenmath is an open source program for symbolic manipulation in math. It runs either in Windows or on a Mac. Some examples of what it can do are shown above.

Peanut math programs

Peanut Math programs

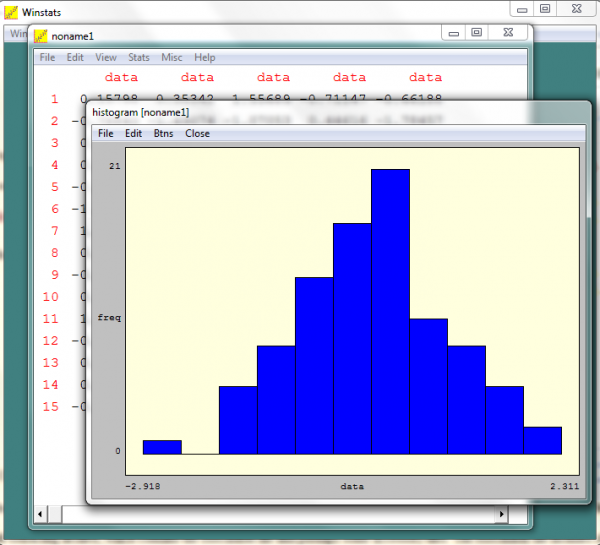
These 9 free programs cover a wide range of different types of mathematics. Above is the popular statistics calculation and visualization program included in the package.

Yacas

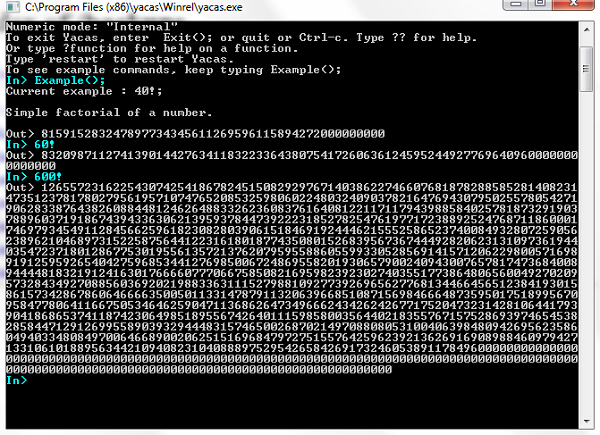
YACAS

Yacas (Yet Another Computer Algebra System) is a command line program which allows for the symbolic manipulation and calculation of mathematical expressions. One thing I like about it is that it calculated 600! in a fraction of a second, so it is very fast (an aside, ever wondered what 6000! factorial is?)

Free CAS programs

Update: Just found an open source implementation of LOGO (as described in Seymour Papert’s Mindstorms) here: http://www.softronix.com/logo.html

Other free programs which I have used either for constructing mathematical diagrams/simulations or with students in some way include:

The Gimp, Programmer’s Notepad, Flex Builder (free with an education license), Open Simulator, VLC PLayer,
Wolfram Demonstrations (requires a free browser plugin), and Project Euler.

You might find these programs as useful alternatives to the “free apps” which “help” students memorize formulas & algorithms. For an enormous list of other free programs see this helpful list.

What other free programs for mathematics education do you use with or for your students?

April 12, 2011 / 2 Comments

How to build an apathetic student body

Here are some of the ways you can ensure your student body is apathetic.

Ignore student voices in important decisions in your schools.
Put up work on the walls students have done for teachers instead of student messages.
Ask for input from students, but make the process nearly impossible or highly exclusive.
Decide that some students have a voice (perhaps because they have a good GPA) but that others don’t.
Blame the students (or their parents) when they are having difficulty learning your course material.
Require students to learn stuff about which they have either no, or limited, choices.

If you watch the video below from TEDxToronto, you’ll see that these very practices are at play in our political spectrum as well.

April 12, 2011 / 0 Comments

Space in the classroom

I watched this video a while ago (recommend watching it, it’s amazing) and was amazed at how you could find spaces in the home where each word was learned. Today I wondered, what would a similar analysis of our classrooms show?

Could you do an analysis to find out where ideas were first learned? Would it vary from classroom to classroom? Could you tell the difference between a classroom based on social constructivism, and another based on behaviourism? How much does the use of our space matter in learning? Would you even be able to assess the learning of a concept in some classrooms using video analysis?

This is just a thought experiment. I don’t have any answers to the questions I’ve posed, but I am curious…

April 12, 2011 / 0 Comments

Exploring algebraic complexity

Here is an idea I am exploring.

I’d like some feedback on this idea. If anyone can point me at research already done in this area, that would be appreciated. My objective is to use this to justify the use of technology in mathematics as a way of reducing algorithmic complexity so that deeper concepts can be more readily understood.

April 11, 2011 / 3 Comments

Bad calculations

Question: If you didn’t know the procedure for addition or multiplication, and lacked numeracy skills, could you catch the errors in the calculations shown here?

This is what happens when you teach computations instead of reasoning. Anyone who looks at 14 x 5 and gets 25 does not have basic numeracy and estimation skills developed, and quite possibly has never used real objects to do multiplication before. The error is not primarily in the calculations that they are doing but in the system that leads them to trust their calculations more than their common sense and intuition about the problem they are working on. This kind of error happens independently of the tool used. If you don’t believe me that students can make similar computational mistakes using a calculator, ask math teachers how often they see 4/8 = 2 and other similar mistakes.

A mathematics curriculum based on the ability to do computations and not solve problems is flawed in my mind. We should focus on mathematics as a tool, rather than mathematics as a goal.

April 11, 2011 / 1 Comment

People change (ps. kids are people)

People change.

Change

(image credit: dhammza)

I’m not talking about the obvious physical characteristics that change about people, but their inner thoughts and feelings, the cognitive abilities that make them sentient. No one is exactly the same their whole lives as no one is immune to the effect of gaining experience and wisdom from life’s experiences. It has been shown time and time again that the assumption that people are static and unchanging is false. People often change in dramatic and unexpected ways.

I have two students this year who have made leaps and bounds in their academic ability, largely because they push themselves much harder this year and generally acting more motivated and energized in class. My colleague at my last school loves to talk about a child who started in 9th grade as one of the least academically able 9th graders and ended up top of his class in Calculus AP by the end of 12th grade.

When I was in public school, I was painfully socially inept and struggled not only to make friends, but even to understand the motivations and social expectations of the people in my life. Now, I’m in an incredibly social profession as a teacher, I’m comfortable presenting to a room full of a hundred people, and I interact with thousands of people in the course of a month. I’ve changed a huge amount.

Not all change is positive growth of course , but we need to recognize that change is not only possible, it is likely. Our educational policies should reflect the ability of people to change.

Is it possible for children in your school to switch tracks? For example, can a child on a less academic path switch to a more academic path and vice versa? Can students choose to switch courses when their needs change? Can they switch what elective courses they take? Do your discipline policies reflect a student who can change, or do they apply penalties using strict criteria which allow for no opportunity for growth on the part of the student? Do you let students know that they are even capable of change?

Most importantly, what opportunities exist in your school to help kids change their own lives?

April 9, 2011 / 3 Comments

Open educational resources

Educators, I have some bad news to give you. You aren’t going to get rich. It doesn’t matter how many of your lessons you carefully hoard, or how many great ideas you keep to yourself, none of that is going to make you rich. You will probably never publish your "book" and you aren’t going to get famous.

You could however make a difference. You could give what you’ve got away for free and help make the world a better place. The technology exists to make it relatively easy to share your project ideas, assessments, lesson plans, curriculum, thoughts, whatever you are working on with students. The problem is right now, not enough educators are sharing what they are doing.

The main reason we as educators do not share more of what we do, is that we lack time. We don’t see the value in sharing what we do because it takes effort to upload & share our ideas, and the return is not immediate obvious. Getting that test written, or deciding what you are going to cover for the next week is tedious. To this I say, let your students help you out. Instead of having your students write summaries and rewrite notes from class, have them share the great ideas you come up with collectively with the world. Enable your students to help you. Petition your administration for collaboration time to polish your ideas with your colleagues and then share the result with the world.

Another reason not to share resources is that what we do is fairly specific to our group of students. Many of us customize what we do to the particular group of students we have. To this I say, share the core of what you are doing then, and not all of the details which make it work for your specific case.

Michael Nielsen makes the case in the TED video for Open Science, but in my mind, the same should hold true for education. The resources you make for your classes should be owned by the public, since in the long run, we all benefit. We need to move toward a more open collective experience in education, an Open Education, rather than our current isolated walled garden approach.

April 7, 2011 / 2 Comments

The Scientific Method and Education

In the video above, shared by Dan Colman this morning on the Open Culture blog, Richard Feynman makes this powerful statement.

It doesn’t make a difference how beautiful your guess is, it doesn’t make a difference how smart you are, who made the guess, or what his name is, if it disagrees with [the] experiment, it’s wrong. – Richard Feynman

How would we apply this to education?

We should look at what is working and decide our policies based on the evidence. We should be looking at data, which should have a broad spectrum of types (just like scientific data has) and use it to help determine policy. We need to hold true to Feynmann’s process as well, which is to make a guess as to what will work, decide what the consequences of those actions would be, and then find a way to determine if this is true or not.

There are a number of initiatives in education which either lack data to support their implementation, or which have contradictory evidence as to their effectiveness. For example, various influential people have been promoting the idea of merit pay for teachers, for which the evidence is inconclusive. In other words, someone had an interesting guess about how education works (teachers will work harder for the chance at more money) and drew the conclusion that student learning would improve as a result (as measured by one form of assessment, a standardized test), and the results of the experiment have not shown a result one way or the other (but have shown that when you dangle a big enough carrot in front of people, they will cheat to get it).

My guess is that the schools that work the best start with the premise that teachers should have sufficient autonomy and support to master their craft, and someone (parents, school, or teachers) provides the resources (food, clothing, shelter, safety, supplies, technology) for their children to succeed. I predict that in such schools you would see higher engagement in learning from administrators, teachers, students, parents, and the community.

Who is willing to do an experiment to see if my guess is right?

March 30, 2011 / 4 Comments

What should be on a high school exit exam in mathematics?

Personally, I think an exit exam for school (an exam a student needs to graduate from secondary school) is not necessarily the best way to determine if a student has been prepared by their school. That aside, some of sort of assessment of what a student has learned from their school, whatever form that would take, should satisfy an important criterion; that the student is somewhat prepared for the challenges that life will throw at them.

A typical high school exit exam is testing a student’s preparation for one component of life, specifically college academics. It seems obvious to me that this narrow definition of "preparation" doesn’t actually prepare students for the challenges of life. A student could quite easily pass the NY Regent’s exam in mathematics, any of the IB mathematics exams, their SAT, and any number of other standardized exams, and not know a lick about how to apply the mathematics they are learning in school to solving problems they will encounter in life.

While this shouldn’t be the only goal for mathematics education from K to 12, it seems to me to be a minimal goal, and one which at which we are failing quite dramaticly. Some evidence of this failure is seen by our mostly innumerate public who; lack basic literacy of graphs & statistics, are largely mathphobic, do not understand probability (casinos are good evidence for this), and generally only use relatively simplistic mathematics in their day to day life for problem solving.

There is nothing inherently wrong with teaching how to do a calculation for it’s own sake, or for sharing some of the beauty and power of mathematics, but it should be framed by the notion that our education of mathematics is intended for a greater purpose. If we only focus on the 4 years people spend in college, we do a disservice to the decades of life they have after college.

M	T	W	T	F	S	S
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

Year: 2011 (page 21 of 28)

Most livable city