In an age where we can provide instantaneous access to high-quality encyclopedias and generate customized user-generated-playlists for a billion people on the fly, we should be able to provide curriculum with more ambitious goals and more customizable content than what is currently provided to teachers. The typical curriculum resources teachers have access to today are not structured so that teachers will actually use them (1) and do not adequately support multiple pathways to support all students.
When I first started teaching, I was given a single sheet of paper by the district supervisor for mathematics with a list of twenty questions on it. He told me, “David, If you can get the kids to answer all of these problems by the end of the year, then you are set.” That was the entirety of the direction I was provided as a first year teacher in terms of curriculum and instruction. It took me weeks to find any textbooks in the school and I didn’t really learn what was on the end of year state assessment until I was scoring my students’ work on it. No first-year teacher should be provided so little direction and support.

Is this curriculum?
In my second year of teaching, I was given a textbook and a pacing guide and told that my job was to “cover the curriculum” and make sure that my students got the same experience as other students in other classrooms. I was told that if my supervisor came and observed me and I was not on pace, then I would be automatically given a poor evaluation.
Neither of these approaches to curriculum support works. Either teachers are expected to each individually recreate the wheel or they are treated as completely incapable of making curriculum choices. Teachers must both have sufficient guidance on what to teach and simultaneously the autonomy to adapt and extend curriculum resources to meet their students’ needs.
There is a mindset across many in the teaching profession that teachers should be both be designers and implementers of curriculum. However as Robert Pondiscio notes in his article, “How We Make Teaching Too Hard for Mere Mortals” (2), this leads to a lot of teachers using Google or Pinterest as a primary lesson planning resource which results in an incoherent experience for children. It also is more likely to lead to lessons where the task hasn’t been fully thought through and so any classroom discussions and potential learning opportunities that are embedded within the lesson are more likely to fall flat.
An example of a resource found via Pinterest (source)
Designing curriculum to support learning is a surprisingly challenging and time-consuming task. Suppose for example that you are designing curriculum for a unit on geometry at the elementary school level. It is highly likely that your curriculum will need to include, for example, pictures of triangles like these ones.
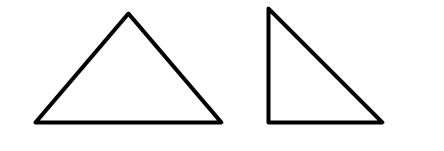
Two triangles in a typical curriculum
There are actually two issues with not being careful about how you use geometric representations with students. If every one of the triangles you draw has one side of the triangle parallel to the bottom of the piece of paper they are drawn on, then students may think that this is a property of triangles. If every triangle has somewhat similar length sides like the ones above then students may think that triangles that look longer and skinnier are not triangles. My own four year old son refers to long skinny triangles as lines, since these triangles have more in common, in his experience, with lines than with the shapes above he happily calls triangles.
Further curriculum is more useful when one lesson deliberately builds on the prior lessons. Teachers often focus on the day to day job of having things to do with students and rarely have the time to deliberately use what they have already done with students and build on their shared experiences. Some mathematical ideas are too big to contain within one lesson, and so planning day-to-day leads to an incoherent experience for children (3).
Curriculum has the potential to offer so much more than just resources for teachers to use in lessons. It can be a tool where they continue the learning about the content they teach that their education schools rarely have time to complete. Across the United States, many teachers now teach out of the content area for which they were trained, and so embedding opportunities to learn this content for teachers is especially important.
When the teachers’ manual, which usually contains somewhat repetitive suggestions for teaching, is only a click away from the resource a teacher is accessing, then learning about pedagogy can more easily be embedded within the curriculum. Deborah Ball is leading a project (4) to determine the highest leverage content (5) and pedagogy to be taught before teachers start teaching. What if curriculum authors were able to carry on this work with in-service teachers? What if the curriculum deliberately and explicitly offered multiple pathways through the curriculum?
One of the major areas I knew almost nothing about when I finished my degree in education was the ways students typically understand and misunderstand mathematics (6). In order to be best positioned to remediate common errors and misconceptions students make while learning mathematics, I need to know both strategies for this remediation and to know the ideas to be remediated. When you look across just the high school mathematics curriculum, the number of different ways students typically understand each mathematical idea varies greatly, and so the sheer amount of information about student understanding that a teacher would need to know is overwhelming. No one has successfully captured all of these ways of knowing yet, but some efforts exist, at least at the elementary school level (7). An ambitious curriculum would keep track of at least some of these common ways of understanding mathematics so that teachers who are planning units can reference these resources on demand.

A sample resource intended to address a misconception (source)
Further when I learned more about actively supporting students in developing productive dispositions towards the mathematics I taught, I learned that framing student ideas as either ‘knowing the math’ or as a misconception isn’t all that helpful. I now think of students as making sense of the world around them and try to figure out how their ideas are logical, given what the children know, rather than try to find the mistakes children make (8). What if the curriculum teachers accessed explicitly offered suggestions on how to improve students’ self-conceptions of themselves as mathematicians?
Teaching in response to what children know or do while working on authentic mathematics tasks (9) is difficult yet most curriculum resources offer almost no support for teachers in doing this. The most common understanding of formative assessment is that it is a type of assessment teachers give in order to determine what children know, but as Dylan Wiliam’s book Embedded Formative Assessment (10) shows, this is a limited definition and perhaps not helpful definition of formative assessment. Given the importance of formative assessment in teaching, strategies for formative assessment, like the 5 Practices for Orchestrating Productive Mathematics Discussions (11), could be embedded right into the planning materials for the curriculum.
Another major area of my own learning was about the use of mathematical representations to support student learning. I knew mathematics and I knew many mathematical representations of that mathematics, but I had not deliberately been exposed to mathematical representations, such as tape diagrams or area models, during my teacher training. An excellent curriculum would support teachers in making explicit connections between different representations and as a result, being better prepared to select mathematical representations to use with their students. Mathematical representations are an excellent tool for students (and their teachers) to make connections between different mathematical ideas and as such should be forefronted in curricular resources. Further, a cohesive curriculum should be written such that the representations that start their use early in a child’s school career make it easier for the same child to make mathematical connections in their future mathematics classes.
Sample representation (source)
When we can provide curriculum electronically, the resources that can be included for any given lesson or activity are limitless, yet we still design most curriculum with the limitations of print. A truly ambitious curriculum would have typical student approaches, useful mathematical representations, suggestions for pedagogy, specific tasks to support a mathematical idea, and other resources all within a click. Why not supply slides and templates for teachers to use so that teachers can focus on other more important aspects of their craft, such as anticipating student thinking for the upcoming lesson?
And it goes without saying that the strategic use of technology should be embedded within the curriculum with the caveat that given the current state of technology across the United States, that curricular resources should work in a variety of contexts. Some schools have one computer per classroom which might be hooked up to a projector, other schools have devices for each child; an ideal curriculum supports all likely arrangements of technology.
In Todd Rose’s The End of Average (12) he recounts a story about the design of the cockpit of an airplane, which I believe should inform curriculum writing:
…
After multiple inquiries ended with no answers, officials turned their attention to the design of the cockpit itself. Back in 1926, when the army was designing its first-ever cockpit, engineers had measured the physical dimensions of hundreds of male pilots (the possibility of female pilots was never a serious consideration), and used this data to standardize the dimensions of the cockpit. For the next three decades, the size and shape of the seat, the distance to the pedals and stick, the height of the windshield, even the shape of the flight helmets were all built to conform to the average dimensions of a 1926 pilot.
…
Out of 4,063 pilots, not a single airman fit within the average range on all 10 dimensions. One pilot might have a longer-than-average arm length, but a shorter-than-average leg length. Another pilot might have a big chest but small hips. Even more astonishing, Daniels discovered that if you picked out just three of the ten dimensions of size — say, neck circumference, thigh circumference and wrist circumference — less than 3.5 per cent of pilots would be average sized on all three dimensions. Daniels’s findings were clear and incontrovertible. There was no such thing as an average pilot. If you’ve designed a cockpit to fit the average pilot, you’ve actually designed it to fit no one.

The cockpit of an airplane (source)
What about curriculum? We all know that children enter classrooms in many different shapes and sizes, and that their understanding of the content we intend to teach is as varied, and yet we design curricular resources that mostly aim to support an average child. What if there is no such average child? The curriculum that aims to best support the average child may in fact support no one best.
It is well-known, for example, that students need multiple opportunities to both learn a mathematical idea and to access their memory of the idea in order to strengthen their memories (13). Almost no curricula deliberately interleave practice or offer opportunities for spaced retrieval practice. What if a curriculum deliberately included ideas from cognitive science into its construction?
There are also strategies for supporting students with special needs and emergent bilingual students which offer additional avenues for students to access the same mathematical content as their peers and which when implemented effectively, support all students. Many curricula offer no deliberate pedagogical suggestions for different populations of students, but in New York City alone there are more than 170,000 students with special needs and over 140,000 (14) students who are learning English as a second language. Given that access to education is a fundamental human right (15), our curriculum resources should offer the greatest possibility that all students have access rather than being a potential limiting factor.

One suggestion for this curriculum is to embed the use of instructional routines (16) throughout. In our work (17) on curriculum we have discovered that instructional routines offer support for teachers and students in multiple ways. Since they routinize the “steps” to a lesson in predictable ways, they allow teachers to focus on the parts of the lesson that change in response to the students and the mathematical ideas presented within the routine structure. Similarly, curriculum developers are able to develop tasks for instructional routines more rapidly and with more confidence that they will be used in the way intended when the possible ways the task will be enacted with children are more narrowly defined. Since students and teachers know what to expect next when the routine unfolds, they can more completely focus on each other and their mathematical reasoning. These routines also allow teachers to learn from their enactment as they “temporarily hold some [parts of their teaching] constant while working on others.” (18) Finally, well designed routines embed formative assessment into the structure of the routine (19) so that the challenging work of responsive teaching becomes more manageable to learn.
Finally, the license and formatting of curriculum resources should encourage both thoughtful revisions to the curriculum and the sharing of those revisions back to the greater community. In the United States, we have a million mathematics teachers, each basically writing lessons and altering resources on their own to support their students’ understanding, and no shared pool of resources from which to iterate. While online communities (20) have sprung up around different instructional routines, there is no policy in place nor organization that has stepped up to help organize those routines and their associated resources into a cohesive collection that can be built upon. Further, access to curricular resources is highly uneven across the many thousands of school districts across the United States, and a more open access model may help mitigate education inequities.
It is not likely that such an ambitious curriculum will emerge on its own. It will require the combined efforts of many hundreds of teachers and curriculum specialists working over a decade or two to design, test, and iterate to create a coherent collection of resources. Educational researchers should be included from the beginning of the curriculum construction so that they can rigorously test the impact of the curriculum on student learning. Professional development providers should be included so that the professional learning experiences of teachers who volunteer to be part of this effort can be aligned to the aims and beliefs about learning embedded within the curriculum structures.
Given that funding for education appears to be already stretched, this additional effort may need to be funded by outside partners. However the potential for such a project to have a long-lasting impact on student learning is great. We already know that curriculum impacts student learning (21); what might be the impact of an ambitious curriculum?
References:
- Meyer, D. (2016). NCTM Puts Up a Sign, Retrieved from http://blog.mrmeyer.com/2016/nctm-puts-up-a-sign/ on September 6th, 2016.
- Pondiscio, R. (2016), How We Make Teaching Too Hard for Mere Mortals, Retrieved from http://educationnext.org/how-we-make-teaching-too-hard-for-mere-mortals/ on September 6th, 2016.
- Daro, P. (2013). Teaching Chapters, Not Lessons, Retrieved from https://vimeo.com/79909978 on September 6th, 2016
- Ball, D. et al. (2013). Teaching Works, Retrieved from http://www.teachingworks.org on September 6th, 2016
-
Ball, D., Hill, H., and Bass, H. (2006), Knowing Mathematics for Teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, 29(1), p. 14-17, 20-22, 43-46., Retrieved from https://deepblue.lib.umich.edu/bitstream/handle/2027.42/65072/Ball_F05.pdf on September 6th, 2016
- Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching what makes it special?. Journal of teacher education, 59(5), 389-407.
- Carpenter, T., Fennema, E., Franke, M., L. Levi, and S. Empson. (2014) Children’s Mathematics, Second Edition: Cognitively Guided Instruction. Portsmouth, NH: Heinemann
- Wees, D. (2015) Mistake Makers or Sense Makers. Retrieved from https://www.youtube.com/watch?v=1N10pp1GdXE on September 6th, 2016
- Lampert, M., Beasley, H., Ghousseini, H., Kazemi, E., Franke, M. (2010) Using designed instructional activities to enable novices to manage ambitious mathematics teaching (pp. 129-141). In M.K. Stein & L. Kucan (Eds.) Instructional explanations in the discipline. New York: Springer.
- Wiliam, D. (2011). Embedded Formative Assessment. Bloomington, Solution Tree.
- Stein, M., Smith. M. (2009). 5 Practices for Orchestrating Productive Mathematics Discussions. Reston, VA. The National Council of Teachers of Mathematics
- Rose, T. (2016) The End of Average. New York, Harper Collins.
- Smith, M. and Weinstein, Y. (2016) Six Strategies for Effective Learning. Retrieved from http://www.learningscientists.org/blog/2016/8/18-1 on September 6th
- Statistical Summaries. (2016), Retrieved from http://schools.nyc.gov/AboutUs/schools/data/stats/default.htm on September 6th, 2016
- The Right to Education. (2016), Retrieved from http://www.unesco.org/new/en/right2education on September 6th, 2016
- Lampert, M., Graziani, F. (2009). Instructional Activities as a Tool for Teachers’ and Teacher Educators’ Learning. Retrieved from http://tedd.org/wp-content/uploads/2014/11/Graziani-Lampert-Instructional-Activities.pdf on September 6th, 2016
- A2i Project (2012 to 2016), see http://math.newvisions.org for resources and further details.
- Lampert, M., Beasley, H., Ghousseini, H., Kazemi, E., Franke, M. (2010) Using designed instructional activities to enable novices to manage ambitious mathematics teaching (pp. 129-141). In M.K. Stein & L. Kucan (Eds.) Instructional explanations in the discipline. New York: Springer.
- Wees, D. (2016). Instructional Routines As Formative Assessment. Retrieved from https://davidwees.com/content/instructional-routines-as-formative-assessment/ on September 6th.
- Welcome to the Math Twitter Blogosphere. (2011), Retrieved from http://mathtwitterblogosphere.weebly.com/ on September 6th, 2016
- What Works Clearinghouse, Interventions in Math, Retrieved from http://ies.ed.gov/ncee/wwc/FindWhatWorks.aspx?o=9&n=Mathematics/Science&r=1 on September 6th, 2016
Susan Jones says:
I have wondered for decades about what you say here:
“It is well-known, for example, that students need multiple opportunities to both learn a mathematical idea and to access their memory of the idea in order to strengthen their memories (13). Almost no curriculums deliberately interleave practice or offer opportunities for spaced retrieval practice. What if a curriculum deliberately included ideas from cognitive science into its construction?”
… and working with students with specific learning disabilities for those decades means that I personally share your frustration with the lack of attention to diverse learners.
So… how to find those partners without getting swallowed up in an agenda that doesn’t support learning?
September 11, 2016 — 5:30 pm
Benjamin says:
How timely. Our district is trying to decide whether to adopt a new middle school curriculum (currently using CMP). The current board I believe just voted to look at the in house curriculum developed at one of the middle schools. At which point I realized another important in any such effort: transparency. I have no window into what they are doing in the building. It could be awesome, it could be less so. In a world beyond publishers its real hard to gauge quality from the outside.
September 12, 2016 — 12:09 am
David Griswold says:
This is a very thoughtful post, filled with great truths. I wonder how an organization capable of fulfilling these needs comes together. Maybe the Illustrative Mathematics team is getting there. Im greatly looking forward to reading their middle school curriculum and I’m also interested to see how flexible they are able to stay in a publilishing environment. And of course I wonder how long their funding will hold out if they distribute free forever, but maybe they have a business model that will work.
My experience with CPM, an organization that has always worked to do many of the things included in this post (including detailed instructional routines, for example, as well as incorporating spaced and interleaved practice) has convinced me that a nonprofit, specialized organization will have an advantage over larger commercial publishers for flexibility. CPM is still a print-first organization, with less flexibility than some more recent groups might have, but the seeds are there; the more articles like this one I read, the more impressed I am by what that team has been quietly doing since the 1980s.
My experience with CPM, however, also makes me wonder how realistic it is to expect any one curriculum could ever be accepted across the board. Curricula are polarizing by their nature. Some teachers/parents/administrators/school boards want a progressive, exploratory approach. Even within that, some prefer a casual, conversational style like that of CPM while others prefer a more formal mathematics style like that of CME. Others are more traditional in mindset; they too will benefit from tasks and problems that are not lazily created, but I’m not sure the same curriculum and instructional routines can support both groups. And new teachers unfortunately don’t usually know what they want; basically no matter what they are told to do they are likely to rebel and flail and cast about as they try to find their own style.
It is a tough problem but I am heartened that so many brilliant people and organizations are starting to tackle it. It seems to be a topic right now; hopefully many will ride the wave long enough to create something better than the historical products.
September 12, 2016 — 12:32 pm
john duffty says:
Others before me have been far more eloquent… All I want to add is that this is by far the most rational post I have read all year. Spot on sir, I’ll be quoting sections of this – and sending people to it – for a very long time.
Brilliant.
September 18, 2016 — 11:06 pm
Chester Draws says:
Educational researchers should be included from the beginning of the curriculum construction so that they can rigorously test the impact of the curriculum on student learning.
More likely hinder it’s useful construction, as they will focus on what is theoretically correct, rather than what actually works. If they weren’t interested in theory they would be teachers, not researchers.
Teachers know what the common misconceptions are, as we meet the same ones time and again.
The issue is how to solve them quickly, without needing to build some theoretical edifice.
For example, that worksheet you show which is meant to teach them to correct way to add fractions is theoretically sound to many researchers. In practical terms it tends to not work because what the child sees most, and therefore remembers most vividly, is the large mistake across the middle. It’s very, very doubtful whether showing a mistake for so long does any good at all.
I don’t care what theory says, never show students how to do things wrong.
If you want a curriculum that works, leave the theorists out. They’ll never agree anyway about anything other than theory.
September 30, 2016 — 10:38 pm
David Wees says:
Hey Chester,
Obviously we disagree on this point. I can see you have your mind made up though so I see little point in discussing this point further.
Suffice it to say that there are some of educational researchers whose work is in fact useful to teachers, regardless of your personal perspective on the matter.
As for never showing a mistake to a student, this particular task is intended to be used after you, a teacher, have noticed your students making errors with a particular operation. It’s not designed by educational researchers, it’s designed by teachers.
David
October 5, 2016 — 3:53 am