A few days ago, my wife told my son that he should do some mathematics from a 2nd grade workbook we had, and told him he could choose what he worked on. My son opened up the book to near the end of the workbook and decided to try some 2 digit subtraction exercises.
Here is an example of his work.
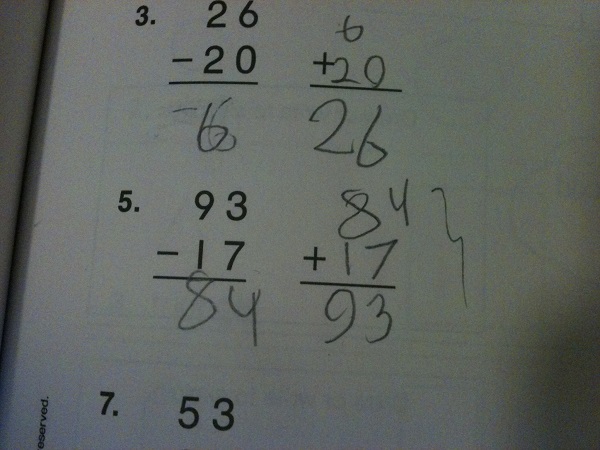
As I often do, I sat down with him and asked him to explain his work (note: I do this whether or not the work is correct). He told me, “Okay. Ninety take-away ten is eighty and seven take-away three is four, so the answer is …” and then he paused, “Okay. Mommy is right the answer is seventy-six.” I asked him why he changed his answer, but he was not able to articulate what made him change his mind.
We talked next about possible strategies we could use to solve this problem.
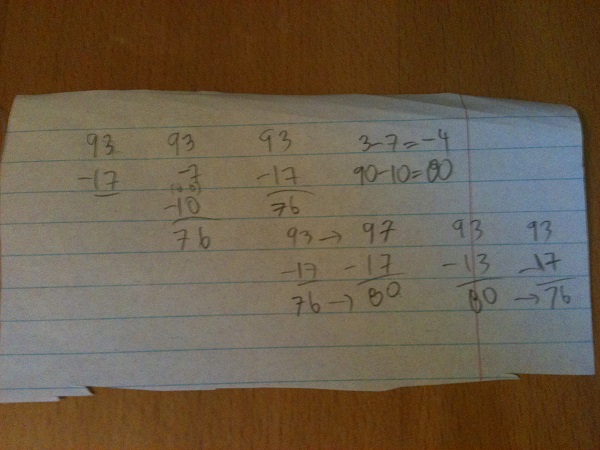
My son said that one way to find the answer would be to subtract seven from ninety-three, which would give eighty-six, and then subtract ten more, which would result in seventy-six. Another strategy he said he could use would be to take seven away from three first, which is negative four. Ten subtracted from ninety would be eighty, and eighty plus negative four would also be seventy-six. I suggested that another strategy could be to change ninety-three to ninety-seven, noting that this should increase the answer to our subtraction by four. Next we would subtract seventeen from ninety-seven, which my son said, “Obviously 97 take-away 17 is 80.” Finally, we need to reduce our answer of 80 by 4, to get a final answer of 76.
You may notice that I have not yet introduced the standard subtraction algorithm that includes borrowing a ten from the ninety, and then doing the subtraction as eighty take-away ten, and thirteen take-away seven is six, leading to a final answer of seventy-six as well. This is because I want to make sure that my son has a good understanding of how subtraction works first, so that I do not end up confusing him with what might other-wise feel like an arbitrary procedure.
Howard Phillips says:
http://mathcomesalive.com/savingschoolmath.doc
Hello David
I have been waiting for a chance to send you my thoughts on the teaching of number in elementary school, which I consider is at present all mixed up. These have been brewing for some months, and I finally got them all together last week. A large chunk is about negative numbers and where they come from.
I am going to email it to you, and you can download from the link above (that’s where the editor put it)
The title is a bit pretentious, but I have more to say on the subject in due course.
January 9, 2014 — 5:24 pm
Howard Phillips says:
In the OLD days we borrowed one at the top and paid it back at the bottom. Agreed it is slightly more complicated than the new improved method, which actually takes the 1 (yes, it is 10 times the value of a one in the current column) away and adds it to the digit in the current column, and there is therefore no paying back to do, but both methods hit a problem when there are zeros or nines around: new method 2006 – 173, old method 2134 – 1692 etc. I am thinking that expecting pupils not only to understand (either) method but also to explain it is asking for the moon. After all, it is a routine or algorithm which when applied correctly gets the correct answer. So long as the pupils understand what subtraction is and can explain it in simple terms, eg stepping along the number line (for natural numbers) then we should all be happy.
An example: I know that the intersections of successive normals to a curve give the evolute. Can I derive the theory? Yes. Can I explain why it works? With difficulty!
January 9, 2014 — 6:50 pm
David Wees says:
Some reasons students should explain their method in a classroom setting are as follows:
January 9, 2014 — 7:24 pm
Howard Phillips says:
Don’t get me wrong. I think it is absolutely necessary to be able to explain what you are doing or how you did it. I am concerned about the demand for explanation of a standard procedure in an assessment situation. Also I do wonder why the kids are made to learn adding columns of numbers, long multiplication, long division etc when techniques for checking the results from a calculator would be far more useful.
January 9, 2014 — 9:24 pm
Leia says:
My basic skills adult group struggled with the ‘borrowin’ alogrithm. BECAUSE it seems arbitary.
Arbitary is easy to forget!
My favourite strategy these days for explaining it would be to turn the ‘diffult’ 93-17 into two easier tasks
(80-10) and (13-7) (doing the ‘borrowing’ explicitly and in full and producing two easier calculations)
80-10 is simply 70 and 13-7 is easy enough even with counting on to get 6 = add them together = 76.
January 10, 2014 — 5:47 am