When I first started tutoring students, I often noticed that they struggled to add fractions. The addition of fractions just did not make sense to them. Part of this is caused by students having a weak understanding of fractions, and part of this is caused by them not understanding why the typical algorithms used to add fractions make sense.
Here is one model that I developed for myself, so that I could understand why addition algorithms for fractions make sense, and then use this model to help students make sense of adding fractions.
Step 1:
Draw a picture to represent each fraction you want to add. So if I want to add 2/3 and 3/4, I would draw the following, making sure to use rectangles which are the same dimensions, since these two fractions must represent a fraction of the same unit (in this case, the rectangle).
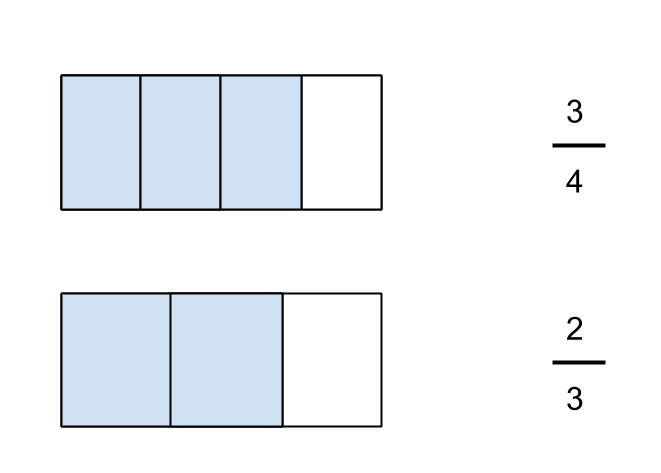
Step 2:
One problem with the above drawing is that it is not the only way to represent fractions. Anticipating that I will want to be able to match units, I realized that it is convenient to draw my fractions with different orientations, as below.
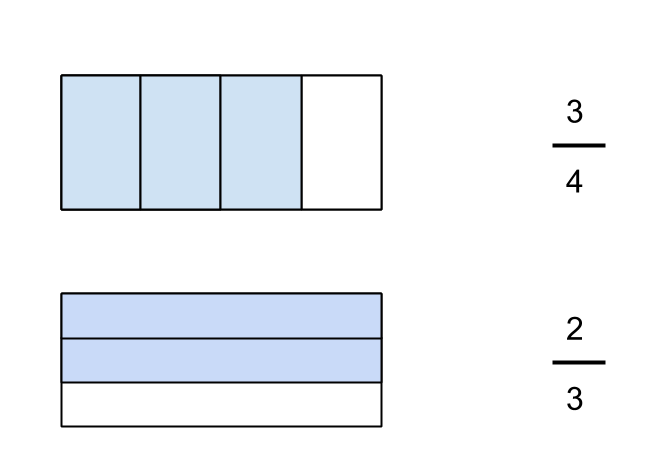
Step 3:
Now, I can’t add the fractions above because the individual pieces of each fraction have different units. I cannot easily see what the total area would be for the two shapes, so I need to divide the two areas again, so that I end up finding the area of each fraction with the same sub-unit of the rectangle (in this case, 1/12).
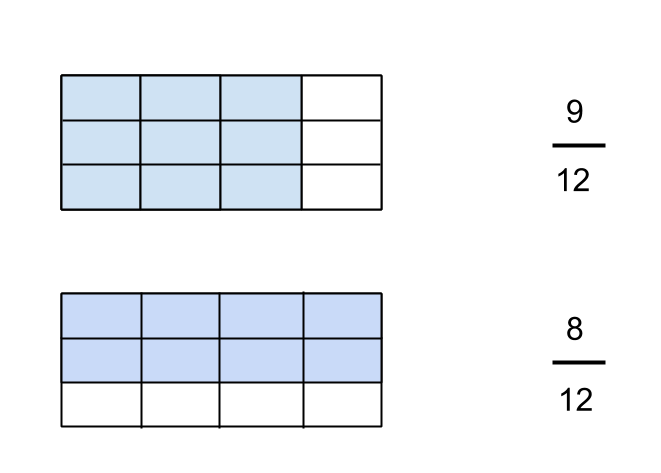
Step 4:
Now that the units of each fraction are the same, I can simply count the total number of units in the first fraction (9) and add it to the total number of units in the second fraction (8), and I arrive at my answer of 17 units. I have to remember though that the size of this unit, relative to the original unit, is a twelth, hence my answer is 17/12 in terms of the original unit.
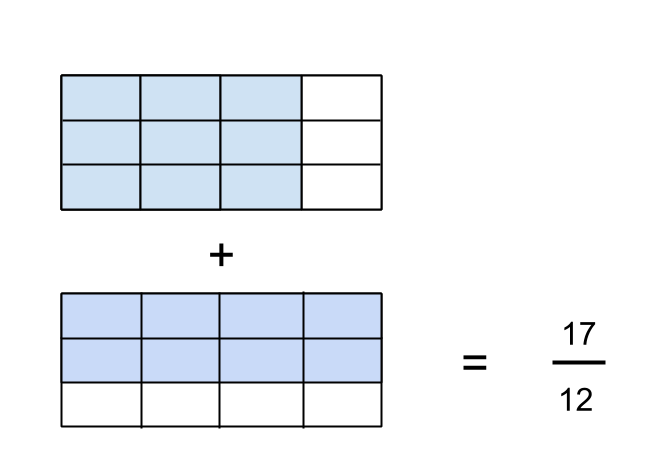
What makes this model difficult to understand, and perhaps this lies at the heart of understanding addition of fractions, is that I have switched from counting in one unit (the whole rectangle), to counting in different units (quarters and thirds), to then counting in yet another unit (twelths), and then being able to see this final total in terms of the original unit (the whole rectangle).
This suggests to me that the prerequisites to understanding fraction addition involve an understanding of what a unit is, understanding how to compose and decompose units, understanding different ways of representing fractions, and how different fractions can be equivalent in size, but measured in different units.
Gregory Olson says:
I’m a student at University of South Alabama getting my degree in Education, and for the class EDM 310 students have to read and respond to a given teacher’s blog. Math was never my strong subject. Though I did not have issues with learning fractions, I never thought about learning fractions in this way. This is, from what I can see, a way of teaching that makes it more accessible to students. I am guessing that this is just a small example of different teaching skills you have learned, and I am wondering if I could use similar techniques when I am teaching English.
February 23, 2014 — 11:15 pm
Wafa Hozien says:
I have a hard time teaching this concept when the student has not understood other basic concepts first. I think it is a developmental stage of learning. I wonder if Piaget did this experiment on his children. Teaching English is an understanding of basic grammatical units as well but need to be used in proper context. Thank you for this basic lesson.
February 25, 2014 — 7:26 pm
NOT SHOWING says:
it helped
September 27, 2018 — 10:54 pm