This video briefly describes how number talks can work, and how they can be implemented in a mathematics classroom.
- Dot patterns

A dot pattern is a visual array of dots, flashed up long enough so that students can see it, but not long enough that they can count it directly. One way to use these patterns is to ask students to come up with how many dots they think they saw, and why they think they saw that many dots. One advantage of dot patterns is that the threshold for the ability for your students to participate is low, and so everyone can more easily see how many different representations are possible.
- Two dimensional patterns
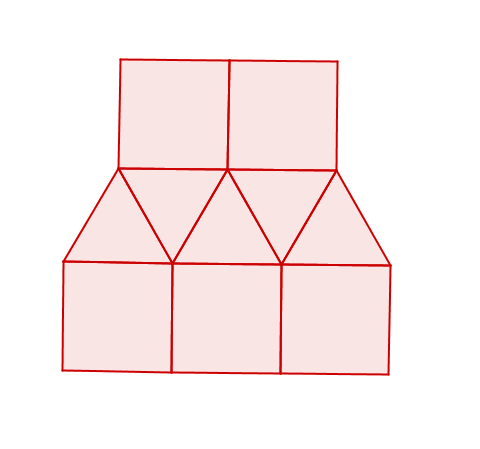
With two dimensional pictures, one objective for students could be to try and reconstruct the picture that is flashed in front of them. Students should try and describe the object using vocabulary they know, and that is as precise as possible to describe the shapes they saw.
- Three dimensional patterns

You can also use three dimensional diagrams in much the same way that you use two dimensional diagrams for math talks. This particular diagram is created in Minecraft, but it is reasonably easy to create a similar diagram using isometric paper.
- Arithmetic problems

Many arithmetic problems would be appropriate for math talks. As a teacher, you might want to select the arithmetic problems based on previous math talks your students have done, so that you have the potential for patterns toi emerge with a series of math talks around arithmetic. Conceptual understanding of a variety of different strategies for solving arithmetic problems will likely help your students develop much needed numeracy skills. Note that it is best to choose problems which can be done mentally by most of your students, so that they have a need to use non-standard algorithms to calculate the arithmetic.
- What’s my rule?
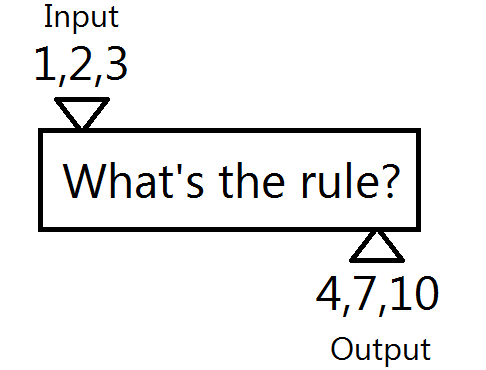
Function machines are also possible, and depending on the function and your goals for the math talk, you can use a variety of different representations in order to display the relationship between the input and output of the function, including, for example, a table of values or a graph. As with all of the math talks, the objective is for students to talk about what evidence convinced them that they knew the function rule, and how they could check that their rule matches the given information.
Some other resources for math talks: